c`est la fonction dérivée de f

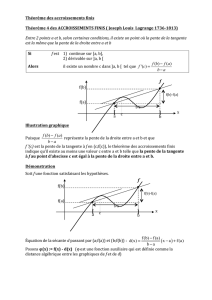
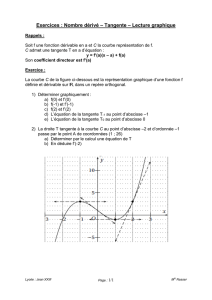
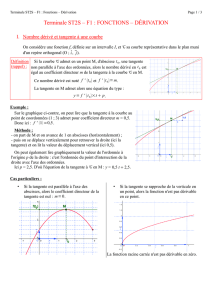
DERIVEE D’UNE FONCTION
1S
Chapitre C3
I)
Nombre dérivé et tangente :
1)
Taux de variation :
Définition : On appelle taux de variation d’une fonction f entre deux valeurs a et b le
f (b)  f ( a )
rapport
.
ba
a) Géométriquement, le taux de variation de f entre a et b représente la pente de la droite
(AB), où A(a ; f(a)) et B(b ; f(b)) sont deux points de Cf.
b) Exemples :

Calculer le taux de variation de f : x
2 x3 entre 4 et 7.
f (7)  f (4) 2  73  2  43 2  343  2  64 558



 186
74
3
3
3

5
entre 1 et 2.
x
5 5

g (2)  g (1)
1  2,5  5  2,5  2,5
 2
2 1
1
1
1
Calculer le taux de variation de g : x
2)
Nombre dérivé :
En rapprochant B de A, la droite (AB) se rapproche de la tangente à Cf en A, et le taux de
variation de f se rapproche de la pente de la tangente.
f ( a  h )  f ( a ) f ( a  h )  f (a )
En écrivant b = a + h et en rapprochant h de zéro, on a :

( a  h)  a
h
qui se rapproche de la pente de la tangente en A.
f ( a  h)  f ( a )
admet une limite lorsque h tend vers 0, on dit que la
h
fonction f est dérivable en a. La limite atteinte est alors appelée nombre dérivé en a et
f ( a  h)  f ( a )
notée f ’(a). On note : f '(a )  lim
.
h 0
h
Définition : Lorsque
Propriété : Lorsque f ’(a) existe, alors c’est la pente de la tangente à Cf en A(a ; f(a)).
Exemple 1 :
a) Calculer le taux de variation de f : x
b) En déduire f ’(0,5).
c) Tracer Cf et Tf (0,5).
d) Quelle est l’équation de Tf (0,5) ?
Exemple 2 :
a) Calculer le taux de variation de g : x
4 x 2  5 entre 0,5 et (0,5 + h).
3
entre -1 et (-1 + h).
x
b) En déduire g’(-1).
c) Tracer Cg et Tg (-1).
d) Quelle est l’équation de Tg (-1) ?
Exemple 3 :
a) Calculer le taux de variation de k : x
b) En déduire k’(5).
c) Tracer Ck et Tk (5).
d) Quelle est l’équation de Tk (5) ?
x3  7 entre 5 et (5 + h).
3)
Equation de la tangente :
Théorème : Soit une fonction f et Cf sa courbe représentative. Si f ’(a) est connu, alors
l’équation de la tangente au point d’abscisse a est : y = f ’(a)(x – a) + f (a)
Preuve : Le point A appartient à la courbe, donc A (a ; f(a)).
On prend un point M (x ; y) sur Tf(a) différent de A ; (AM) a pour pente f ’(a).
y  f (a )
On a donc : f ' (a ) 
donc y – f(a) = f ’(a)(x – a) puis y = f ’(a)(x – a) + f (a)
xa
4)
Approximation affine d’une fonction en un point :
Erreur = distance MP
Autour du point A (a ; f(a)), la courbe Cf et la tangente Tf(a) sont très proches.
L’écart entre f(x) (valeur exacte de la fonction) et f ’(a)(x – a) + f (a) (valeur approchée de la
fonction) est d’autant plus petit que x est proche de a.
En notant h = x – a, on a : f (a  h)  f (a)  f '(a)h (valable seulement pour h petit)
f (a)  f '(a)h est l’approximation affine locale de f (a + h).
II)
Fonction dérivée f ’ :
1)
Définition :
Définition : Soit une fonction f définie sur un intervalle I. On dit que f est dérivable sur I si f
admet un nombre dérivé f ’(x) en tout x de I. On note f ’ la fonction ainsi obtenue : c’est la
fonction dérivée de f (« f prime »)
2)
Exemple :
Soit f : x
x2  1 définie sur
. On prend une valeur a
au hasard.
f (a  h)  f (a) [(a  h)2  1]  [a 2  1] a 2  2ah  h 2  1  a 2  1 2ah  h 2



 2a  h
h
h
h
h
Donc
f ’(a) = 2a
(vrai pour tout valeur réelle de a !)
La fonction x 2x donne donc f ’(x) à chaque fois.
Donc f : x x2  1 admet pour fonction dérivée f ' : x
3)
Dérivées des fonctions usuelles :
f (x)
constante k
x
ax + b
x²
x³
n
x , avec n  N *
1
x
1
, avec n  N *
xn
x
sin x
(x en radians)
cos x
(x en radians)
4)
Règles de calcul :
a)
Somme :
f ’(x)
0
1
a
2x
3x²
nx n1
1
 2
x
n
x n 1
1
2 x
cos x
Intervalle de validité
;0 ou 0;
;0 ou 0;
0;
– sin x
Théorème : Si u et v sont dérivables sur I, alors :
b)
2x .
(u + v)’(x) = u’(x) + v’(x)
Produit :
Théorème : Si u et v sont dérivables sur I, alors :
(uv)’(x) = u’(x)v(x) + u(x)v’(x)
En particulier :
 (ku)’ = ku’ pour k une constante réelle.
 (u²)’ = 2uu’ (conséquence du théorème avec u = v)
Exemple :
Soit f : x
(4 x 2  3)(5  x) ; on pose u(x) = 4x² – 3 et v(x) = 5 – x →
f '( x)  u( x)v '( x)  u '( x)v( x)  (4 x 2  3)(1)  (8x)(5  x)  4 x 2  3  40 x  8x 2  12 x 2  40 x  3
c)
Inverse et quotient :
Théorème : Si v est dérivable sur I avec v( x)  0 sur I, alors :
1 I v '
F
G
Hv J
K v
u I u' v  uv '
F
G
Hv J
K v
'

2
'

2
Exemples :
(2) Soit g : x
g '( x)  5 
(1) Soit f : x
1
v '( x)
3
; on pose v(x) = 3x – 7 → f '( x)  2

3x  7
v ( x)
(3x  7) 2
5
 1 
; on a : g ( x)  5   2
 →
2
7x  2
 7x  2 
v '
14 x
70 x
 5 

2
2
2
v
(7 x  2)
(7 x 2  2)2
3x  2
; on pose u(x) = 3x – 2 et v(x) = 10x – 7 →
10 x  7
u ' v  uv ' 3(10 x  7)  10(3x  2)
1
h '( x) 

 ... 
2
2
v
(10 x  7)
(10 x  7) 2
(3) Soit h : x
d)
Dérivabilité :
Pour utiliser les formules de dérivation précédentes, il faut d’abord régler le problème de leur
validité (sur quel domaine peut-on dériver ?).
Propriété :
1) Les fonctions polynômes sont définies et dérivables sur .
2) Les fonctions rationnelles sont dérivables sur leur ensemble de définition.
Exemples de rédaction :
(1) f ( x)  7 x10  x7  18 ; f est une fonction polynôme, donc f est définie et dérivable sur
→ f ' ( x)  70 x9  7 x6
15  x
(2) g ( x) 
; (v.i.) 16  x 2  0 ; x 2  16 ; x = 4 ou x = – 4 ; donc Dg 
16  x 2
g est une fonction rationnelle donc g est dérivable sur  4;4 .
u(x) = 15 – x → u’(x) = – 1
v(x) = 16 – x² → v’(x) = – 2x
 4;4
.
→ g ' ( x) 
e)
1(16  x 2 )  (2 x)(15  x)  x 2  30 x  16

(16  x 2 ) 2
(16  x 2 ) 2
Dérivée de g telle que g(x) = f (ax + b) :
Théorème : Soit f une fonction dérivable sur I, et g la fonction définie par g(x) = f (ax + b).
Alors g est dérivable pour tout x tel que ax + b appartient à I, et g ' ( x)  af '(ax  b)
Exemples :
(1) Soit g : x
(4 x  20)12 ; on pose f ( x)  x12 → g ' ( x)  4 f '(4 x  20) avec f '( X )  12 X 11
On remplace X par 4x + 20 ; on trouve : g ' ( x)  4 12(4 x  20)11  48(4 x  20)11
(2) Soit g : x
cos(2,5 x  7) ; on a :
g ' ( x)  2,5 f '(2,5x  7)  2,5  [ sin(2,5x  7)]  2,5sin(2,5x  7)