QCM. Electrostatique

PCSI. 01-02.
QCM. Electrostatique
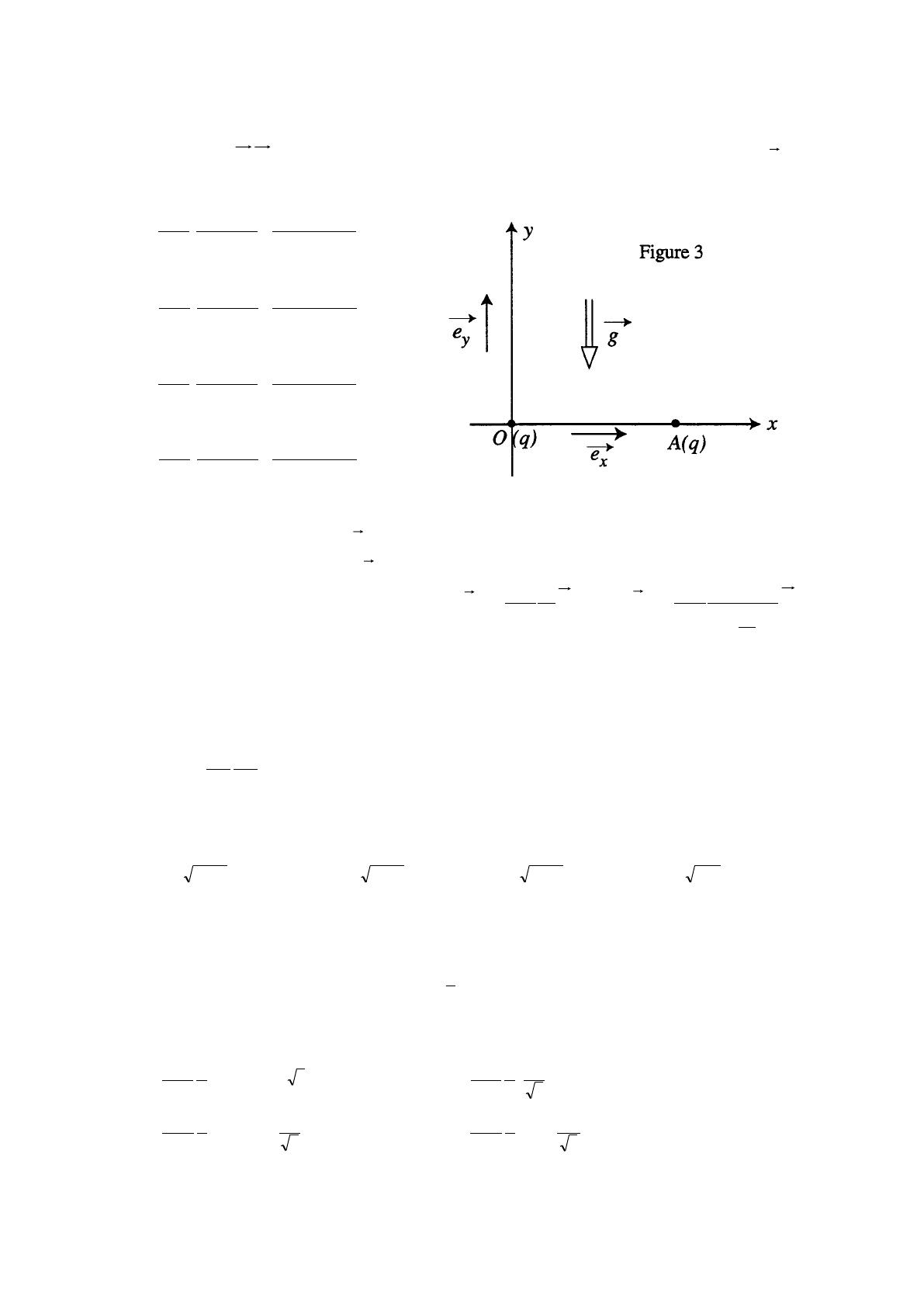
1.
Deux charges électriques ponctuelles identiques q sont placées respectivement à l'origine O et au point A (a> 0, 0)
du repère plan (O; ex ; ey ) (fig. 3). Calculer les composantes Ex et Ey du vecteur champ électrostatique E(P) créé
au point P du plan, de coordonnées x et y .



q 
x

a
x

a) Ex=
4 0  x 2  y2 3/ 2 xa 2  y2 3/ 2 









q 
x

a
x

b) Ex=
3/ 2
3/ 2 

2
2
2
4 0 x  y
xa   y2 









q 
y
y

c) Ey=
4 0  x 2  y2 3/ 2 x a 2  y2 3/ 2 



d) Ey=
2.






q 
y
y

4 0  x 2  y2 3/ 2 x a 2  y2 3/ 2 






Indiquer sur quelle droite  du plan, E(P) est parallèle en tout point à l'axe Oy.
Donner l'expression correspondante de E(P) .
a)  : droite x=a/2
3.
b)  : droite x=y
c) E(P)
q 1
ey
4 0 y 2
d) E(P)
q
2 0
y
ey
a2
3
/
2
2
(y  )
4
Une charge électrique ponctuelle q' de masse m et de signe contraire à celui de q se déplace sans frottement sur la
droite  à proximité immédiate de l'axe Ox (lyl « a) sous l'action de la force électrostatique due au champ des
deux charges q et de son poids. Oy est la verticale ascendante et g est l'accélération de la pesanteur supposée
uniforme.
qq'
On pose k   4
. Constater qu'il existe une position d'équilibre Pe et calculer l'ordonnée ye de Pe.
 0 a3
a) ye = mg/k
b) ye = -mg/3k
c) ye = -mg/k
d) ye = -mg/4k
4.
Calculer la période To des oscillations qu'effectue la charge q' écartée de sa position d'équilibre.
a) To = 2 m / 4k
5.
b) To = 2 m / 2k
c) To = 2 2m/ k
d) To = 2 m/ k
La charge q' est maintenant fixée au point B(0, a). Calculer l'énergie électrostatique Ue de la famille des trois
charges q en O , q en A et q' en B . L' origine des potentiels est à l'infini. On rappelle que dans le cas d'une famille
de population n :
Ue  1
2
i n
q V
i i
i 1
où Vi est le potentiel créé au point où se trouve la charge qi par les (n -1) autres charges de la famille.

a) Ue  1 1 q'2 2qq' q2 2
4 0 a



c) Ue  1 1 q2 qq' (1 1 )
a
4 0 
2 
 q'2

b) Ue  1 1  2qq' 
8 0 a  2

qq'


d) Ue  1 1 q'2 
q 2 
a
4 0 
2

6.
Donner l'expression de q' en fonction de q pour que l'énergie Ue soit nulle.
a) q ' q 2
b) q' q
2
2 1
c) q' q
d) q' q(2 2 1)
7.
On considère un cylindre infini de rayon R, d’axe de révolution Oz constitué de charges réparties avec la densité
volumique uniforme . On travaille dans la base cylindro-polaire. Le champ électrique E en un point intérieur M à
la distance r de l’axe Oz s’écrit :
a)
b)
c)
d)
 1
er
2 o r

E
rer
2 o

E
rer
2 o
 R
E
er
2 o r
E
8. Deux cylindres identiques C1 et C2, identiques, de rayon R, dont les axes, parallèles au vecteur
ez , sont distants de
a = O1O2 < 2R et portent des charges électriques égales et opposées, uniformément réparties dans tout le volume. On
désigne par 1=  et 2=-  les densités volumiques portées respectivement par C1 et C2. Le champ électrique total
créé par les charges portées par l’ensemble des deux cylindres en un point M du volume défini par l’intersection de C1
et C2 s’écrit :
E 0

O1O2
b) E 
2 o
a)
c)
E
 O1O2
2 o O1O2
d)
E
 O1O2
2 o (O1O2 ) 2
9. Une sphère de rayon b porte une charge Q répartie uniformément sur sa surface. En s’aidant du théorème de Gauss,
calculer le potentiel V créé par la charge Q à l’intérieur de la sphère en un point M à la distance r du centre. L’origine
des potentiels est prise à l’infini.
a) V  0
Q 1
4 o b
Q b
c) V 
4 o r
Q b
d) V 
4 o r 2
b)
V