Exercice 2 chute d`une balle de ping pong Correction

Corrigé exercice II : Chute d'une balle de ping-pong
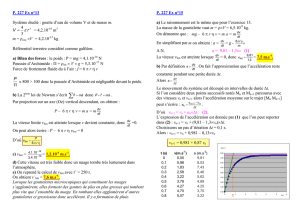
1) Une des courbes correspond à la variation de la valeur v de la vitesse de la balle, l’autre courbe à la
variation de la valeur a de son accélération.
Or, puisque les vecteurs correspondants sont de même sens et même direction lors de la chute, on peut
écrire a = dv/dt.
Or la courbe 1 tend vers une asymptote horizontale (de pente nulle), donc sa dérivée tend vers 0.
La courbe 2 qui est croissante ne peut donc pas correspondre à la dérivée de la courbe 1.
Par contre la courbe 1 correspond à a , et c’est la dérivée de la courbe 2 qui correspond à v.
2) Les valeurs du poids et de la poussée d'Archimède sont indépendantes de la durée de chute.
Par contre la valeur de la force de frottement est proportionnelle au carré de la vitesse.
A l'instant initial, la vitesse est nulle donc F = 0, ceci correspond au schéma de Benoît.
En comparant la longueur du vecteur
F
, on constate que
F
a une valeur F plus grande sur le schéma
d'Amélie par rapport au schéma d'Adrien. Donc le schéma d'Amélie correspond à un temps de chute plus
grand (t2=2,0s) et celui d'Adrien correspond à un temps de chute intermédiaire (t1=0,5s).
3) P = mballe.g
3
4
. . . . .
3
fluide air S air
m g V g r
.g
3
3
P
4 . .
balle
air
m
r
=
32
3
)10.9,1(3,14 10.3,23
= 62
4) Système : balle de ping-pong Référentiel : terrestre (supposé galiléen)
Inventaire des forces : poids et frottement de l'air (poussée d'Archimède négligée face à ces 2 forces)
D'après la deuxième loi de Newton:
amFP .
Par projection sur un axe vertical orienté positivement vers le bas : m.g  F = m
vd
dt
5) Pour t > 2 s, le régime permanent est atteint, alors v = vlim = 8,0 m.s1
La dérivée d’une constante est nulle, donc l’équation précédente devient : m.g  F = 0
m.g – k.vlim² = 0 donc m.g = k.vlim2 et k =
lim
m.g
v²
k =
3
2,3.10 9,8
8,0²
= 3,5.104 S.I.
L'équation m.g  F = m
vd
dt
peut s’écrire m.g  k.v² = m
vd
dt
soit g 
k.v²
m
=
vd
dt
En remplaçant k par son expression: g 
lim
m.g .v²
m.v ²
=
vd
dt
soit
vd
dt
= g –
lim
g.v²
v²
vd
dt
= 9,8 
9,8
8,0²
.v² = 9,8 – 0,15.v²
6) kth = 0,22. .r²
kth = 0,22 1,3(1,9.102)² = 3,2.104 S.I.
On a obtenu kexp = 3,5.10–4S.I. soit k = 0,2.104 S.I. et k/k = 0,2.104 /3,2.104 = 6.10–2 soit 6%
8) La tangente à la courbe représentative de v = f(t), en t = 0 s, coupe l'asymptote horizontale
d'équation v = vlim pour t = . On lit  = 0,8 s.
Le choix du pas d’itération est bon car t << .(réponse tirée d’un corrigé d’annale du BAC)

9) Calcul de a1 :
D'après l'équation
vd
dt
= 9,8 – 0,15.v²
a1 =
1
v
t
d
dt
= 9,8 – 0,15.v1²
a1 = 9,8 – 0,15  (0,49)²
a1 = 9,76 m.s–2
Calcul de v2 :
En considérant
vd
dt
v
t
v = v2  v1 = (9,8  0,15.v1²).t
v2 = (9,8  0,15.v1²).t + v1
v2 = (9,8  0,15  0,49²)  0,05 + 0,49
v2 = 0,98 m.s–1
Calcul de a3 :
a3 =
3
v
t
d
dt
= 9,8 – 0,15.v3² = 9,8  0,15(1,4610227)² donc a3 = 9,48 m.s2
Calcul de t5 : t5 = t4 + t = 0,20+0,05 = 0,25s
10) Il faut conserver autant de chiffres après la virgule de façon à limiter les erreurs, compte tenu du
nombre considérable de calculs intermédiaires nécessaires pour progresser de ligne en ligne. Il est bien
évident que dans le résultat final, seuls les chiffres significatifs en accord avec la précision des données
(dans cet exercice, 2 chiffres significatifs) doivent être conservés.
11) On obtient des courbes théorique et expérimentale similaires.
Il faudrait cependant diminuer la valeur du pas t pour améliorer la concordance.
On pourrait tester comme autre modèle une force de frottement proportionnelle à la vitesse.
L'équation différentielle deviendrait alors: dv/dt = 9,8  K.v avec K différent de k.
a1 = 9,76
v2 = 0,98
a3 = 9,48
t0 =
t1 =
t2 =
t3 =
t4 =
t5 =