TS nombres complexes Amar 15-16

TS. NOMBRES COMPLEXES.
I. Introduction. On rappelle la chaine d’inclusions suivantes : ℕ⊂ ℤ⊂ ℚ ⊂ ℝ
- L’équation x + 3 = 1 n’admet pas de solutions dans ℕ. Elle en admet dans ℤ.
- L’équation 7x − 3 = 1 n’admet pas de solutions dans ℤ. Elle en admet dans ℚ.
- L’équation x ² = 2 n’admet pas de solutions dans ℚ. Elle en admet dans ℝ.
- L’équation x ² + 1 = 0 n’a pas de solutions dans ℝ.
II. Ensemble des nombres complexes et plan complexe.
1. Ensemble des nombres complexes.
Théorème (Admis)
Il existe un ensemble de nombres contenant ℝ, noté ℂ, dont les éléments sont appelés les nombres
complexes et qui vérifie :
- ℂ est muni d’une addition et d’une multiplication qui prolongent celles de ℝ et qui vérifient les
mêmes règles de calcul.
- ℂ contient un élément noté i tel que i ² = - 1.
- Tout nombre complexe z s’écrit de façon unique sous la forme z = a + bi où a et b sont des réels.
2
Exercice. Résoudre dans ℂ les équations : a) x ² = − 1 b) x ² + 4 = 0 c) (x + 1) = −9
2. Forme algébrique d’un nombre complexe.
Définitions. 1
Soit z un nombre complexe. z s’écrit z = a + bi où a et b sont des réels.
• L’écriture a + bi s’appelle la forme algébrique de z.
a est la partie réelle de z. on note Re(z ) = a .
b est la partie imaginaire de z. on note Im (z ) = b .
( La partie imaginaire d’un nombre complexe est un nombre réel)
• Soit z un nombre complexe s’écrivant sous la forme algébrique z = a + bi .
Le nombre complexe a − bi , noté z , est le conjugué de z.
Exemple. Soit z = 3 − 2i . On a alors Re(z) = 3 , Im(z) = - 2 et z = 3 + 2i
Remarque : De l’unicité de l’écriture algébrique d’un nombre complexe, on déduit que deux nombres
complexes sont égaux si, et seulement si, ils ont la même partie réelle et la même partie imaginaire.
Définitions 2.
- Un nombre complexe dont la partie réelle est nulle est appelé imaginaire pur.
- Un nombre complexe dont la partie imaginaire est nulle est appelé nombre réel.
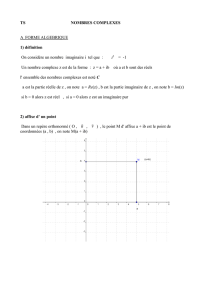
3. Représentation graphique d’un nombre complexe.
r r
On munit le plan d’un nombre d’un repère orthonormé direct (O ; u; v ) .
A chaque complexe z = a + bi où a et b sont des réels, on peut associer le point M (a ;b ) du plan et
réciproquement.
1
On dit que :
● Le point M est l’image du nombre complexe z. On note M (z )
Le vecteur
; est l’image du nombre complexe z. On note
● z est l’affixe du point M. z est aussi l’affixe du vecteur
r
● l’axe des abscisses représente l’ensemble des nombres réels. (O; u ) est l’axe des réels.
● l’axe des ordonnées représente l’ensemble des imaginaires purs. ; est l’axe des imaginaires purs.
r r
● le plan muni du repère (O ; u; v ) et où sont représentés les complexes est alors appelé le plancomplexe.
Exemple et illustration.
Dans le plan complexe ci-contre :
- Le point M est l’image du nombre complexe 3 2 .
- Le vecteur 3; 2 est l’image du nombre complexe 3
2.
- Le nombre complexe 3 2 est l’affixe du point M.
C’est aussi l’affixe du vecteur 3; 2
III. Opérations dans ℂ.
1. Addition.
Théorème.
Soient z = a + bi et z’ = a’ + b’i deux nombres complexes d’images et
On a alors
● Re (z + z ') = Re (z ) + Re (z ') et Im(z + z ') = Im (z ) + Im(z ') .
● L’image de z + z’ est + ′
′ dans le plan complexe.
Démonstration.
● z + z’= (a + a’) + (b+ b’)i (a + a’) et (b+ b’) étant réels, par l’unicité de la forme algébrique, on en déduit
que Re (z + z ') = Re (z ) + Re (z ') et Im(z + z ') = Im (z ) + Im(z ')
● L’image de z + z’ dans le plan complexe a pour coordonnées ((a + a’) ; (b+ b’)).
Par ailleurs, et ′étant les images de z et z’, on a (a ;b) et ’ (a’ ;b’).
Donc ( + ′)((a + a’) ; (b+ b’)). On en déduit que ( + ′) = .
Définition.
L’opposé d’un nombre complexe z est le nombre complexe z’ tel que z + z’ = 0.
L’opposé de z est noté –z.
Théorème.
Soit z = a + bi un nombre complexe sous la forme algébrique.
L’opposé de z est
Preuve.
z + (-a –bi) = a + bi+(-a –bi)= a + bi-a –bi = 0
Représentation graphique.
Soit A et A’ les images respectives d’un complexe z et de son opposé dans le plan complexe.
A et A’ sont alors symétriques par rapport à l’origine.
Définition.
Soient z et z’ deux complexes. z -z’ désigne le complexe z +(-z’).
2
Théorème.
Soient M et M ’ deux points du plan ayant pour affixes respectives z et z’.
Alors
′ a pour affixe z’- z.
Preuve. Soient a + bi et a’+ b’i les formes algébriques respectives de z et z’.
On a alors z’ -z = (a’ -a) + (b’-b)i . Cette écriture étant la forme algébrique de z’ - z.
Ainsi l’affixe de z’ -z a pour coordonnées
;
Or, M (a ;b) et M ’(a’ ; b’) donc
′
; ′
. On a donc
′.
2. Multiplication.
La multiplication et l’addition dans ℂ suivent les mêmes règles que dans ℂ en tenant compte de l’égalité
i ² = −1 pour simplifier les calculs. Ainsi :
Si z = a + bi et z’ = a’ + b’i sont deux nombres complexes données sous la forme algébrique, alors
z z’ = (aa '− bb ') + (ab '+ a 'b )i
Théorème. Tout nombre complexe z non nul admet un inverse noté
1
.
z
C’est l’unique complexe z’ tel que z z’ = 1
Preuve. Soit complexe z non nul de forme algébrique a + bi.
étant non nul, a et b ne sont pas tous les deux nuls. Donc ²
²
a
b
On vérifie alors aisément que
−
i est l’inverse de z :
a ² +b² a ² +b²
0
b
a²
ab
ab
b²
a²
b²
a ² +b²
 a

−
i  (a + bi ) =
+
i−
i−
i² =
+
=
=1

a ² +b² a ² +b² a ² +b² a ² +b²
a² +b² a ² +b² a ² +b²
 a ² +b² a² +b² 
Exemple. L’inverse de 1+ i est
1 1
− i . En effet,
2 2
1 1 1 1
1 1
1 1 
 − i  (1 + i ) = + i − i − i ² = + = 1
2 2 2 2
2 2
2 2 
Définition.
Pour tous nombres complexes z et z’ avec z’ non nul, le quotient de z par z’, noté
IV. Forme trigonométrique des nombres complexes.
1. Module et argument d’un nombre complexe.
Définition.
Soit z un nombre complexe non nul d’image M dans le plan complexe.
Le module de z, noté | | est défini par | |
Soit θ une mesure de l’angle de vecteurs !" ;
#.
θ est un argument de z. On le note %& . Ainsi, arg
3
* 2+
z
z
1
est défini par
=z×
z'
z'
z'
Théorème.
Soit z un nombre complexe non nul de forme algébrique z = a + bi .
Alors z = a ² + b ²
Preuve immédiate avec la représentation géométrique.
3. Forme trigonométrique d’un nombre complexe.
Soit z un nombre complexe non nul de forme algébrique z = a + bi .
Soit M l’image de z dans le plan complexe. Posons | |
,.
On a alors -
,./0*
, sin *
On a donc z = a + bi = r cos θ + ir sin θ = r (cos θ + i sin θ ) . D’où le théorème :
Théorème.
Tout nombre complexe non nul z s’écrit sous la forme z = r (cos θ + i sin θ )
où r = z et θ est un argument de z.
Théorème réciproque.
Soit z un nombre complexe s’écrivant sous la forme z = r (cos θ + i sin θ ) avec , ∈ ℝ∗5 et *7ℝ.
Alors, r = z et θ est un argument de z.
Exemple. Ecrire sous la forme trigonométrique z = −1 + i .
z = (−1)² + 1² = 2.
− 2
 −1
 
1 
2 
π
π 

z = −1 + i = 2 
+
i  = 2 
+
i  = 2 cos π −  + sin π −  i 

 2
 2
 
2 
2 
4
4 
  3π 
 3π  
z = 2 cos   + sin   i 
4 
  4 
4. Affixe d’un vecteur.
Théorème.
Soit z un nombre complexe non nul d’image
Alors | | ‖ ‖ et arg
= " ; 2+
r r
dans le plan muni d’un repère orthonormé direct (O; u; v ) .
5 . Egalité de deux nombres complexes.
Rappels. L’écriture algébrique d’un nombre complexe est unique. Donc pour tous réels a, b, a’ et b’,
a = a '
a = 0
a + bi = a '+ b ' i ⇔ 
En particulier, a + bi = 0 ⇔ 

b = b '
b = 0


Théorème. Soient z et z ' deux nombres complexes non nuls.
= ⇔ | | = | ′| et ,:
= ,: ’ + 2<+ avec < ∈ ℤ.
Théorème. Soit z un nombre complexe non nul.
∈ ℝ ⇔ ,:
= 0 + <+ avec < ∈ ℤ.
=
z est un imaginaire pur ⇔ ,:
= > + <+ avec < ∈ ℤ.
4
Preuve : z étant non nul, écrivons z sous forme trigonométrique. z = r ( cos θ + i sin θ ) .
∈ ℝ∗ ⇔ sin * = 0
∈ ℝ∗ ⇔ * = 0 + <+ avec < ∈ ℤ.
=
?0 "@ A : @ ,?B", ⇔ cos * = 0, ce qui équivaut à * = > + <+ avec < ∈ Z.
V. Conjugué d’un nombre complexe.
1. Définition.
Soit z = a + bi un nombre complexe sous la forme algébrique.
On appelle conjugué du complexe z, le complexe noté z égal à a – bi.
Exemples. 1 + 2i = 1 − 2i ; −1 − 3i = −1 + 3i ; 2 = 2 ; −5i = 5i .
Représentation graphique.
Un nombre complexe et son conjugué ont des images dans le plan complexe symétriques par rapport à
l’axe des réels.
Propriétés du conjugué.
Théorèmes.
► Soit z un complexe.
a) z = z ; z + z = 2 Re(z ) ; z − z = 2 Im(z )i ; zz = ( Re(z ) ) ² + ( Im(z ) ) ² = z ²
z est un réel ⇔ z = z ;
z est un imaginaire pur ⇔ z = −z
► Pour tous nombres complexes z et z ' :
z + z ' = z + z ' ; zz ' = z z ' ; Pour tout entier naturel n non nul z n = z
1 1
z ' z '
Si z est non nul, alors   = et   = .
z  z
z  z
n
Démonstrations.
► Soit a + bi la forme algébrique de z .
(
)
z = a + bi = (a − bi ) = a + bi = z
z + z = a + bi + a − i = 2a = 2 Re(z ) ; z − z = a + bi − (a − bi ) = 2bi = 2 Im(z )i
z est un réel ⇔ Im(z ) = 0 ⇔ 2 Im(z ) = 0 ⇔ z − z = 0 ⇔ z = z .
► Soient respectivement a + bi et a’ + b’i les formes algébriques de z et z ’.
Somme : Immédiat.
Produit : Immédiat avec les formes algébriques.
n
z n = z par récurrence sur n.
 1
1
1 1
1 = 1 =  z ×  = z ×   d’où   = .
 z
z 
z  z
1
1 z'
z ' 
1
  =  z '×  = z ' ×   = z ' × =
z
z z
z  
z 
5
VI. Propriétés des modules.
1. Conséquences immédiates de la définition.
Théorèmes.Pour tout nombre complexe z,
z ² = zz
z =0⇔ z=0
z = z = −z
Démonstrations immédiates d’après la définition : Soit a + b i l’écriture algébrique de z.
● z z = a² + b² = z
z = 0 ⇔ a ² + b² = 0
z = 0 ⇔ (a = 0 et b = 0)
●
z =0⇔ z=0
2. Modules et opérations.
Théorème. Pour tous nombres complexes z et z’ :
• | | = | || |
• Pour tout @ ∈ ℕ∗ , | F | = | |F
|H|
H
J
J
• Si ≠ 0, GHI G = |HI |. En particulier, GHI G = |HI |
• | + ′| = | | + | ′|
Démonstrations.
•
zz ' =
zz ' zz ' =
zz ' z z ' =
z zz ' z ' =
z ² z' ² = z z' .
• « Pour tout @ ∈ ℕ∗ , z n = z n » se démontre par récurrence.
Pour n = 1. z1 = z et z 1 . On a donc z1 = z 1 et la propriété est vraie au rang 1.
Soit un entier naturel non nul k. Supposons que la propriété est vraie au rang k : c-à-d : z k = z k .
z k = z k ⇒ z k z = z k +1 . Or z k z = z k × z = z k +1 .
On en déduit donc que z k +1 = z k +1 ce qui signifie que la propriété est vraie au rang k +1.
On conclut par récurrence que pour tout entier non nul n, z n = z n .
• Pour tout complexe non nul z,
z
=
z'
z  z 
×
=
z '  z ' 
z
z
× =
z' z'
zz
=
z'z'
z²
z
=
z' ²
z'
• Soient M et M’ les images respectives
zret z’uuuuu
dans
uuur de
uuuu
r le plan complexe.
Considérons le point N tel que ON = OM + OM ' .
uuur
L’affixe du vecteur ON est z + z’. Dans le triangle OMN, ON ≤ OM + MN .
Or, MN = OM’ ; OM = z et OM ' = z ' .
On en déduit successivement que ON ≤ OM + OM ' puis z + z ' ≤ z + z ' .
6
Interprétation géométrique du module de la différence.
Soient M et M’ les images respectives de z et z’ dans le plan complexe.
uuuuur
On a alors : z − z ' = MM ' = MM ' .
VII. Propriétés des arguments.
1. Conséquences immédiates de la définition.
Théorème.
Pour tout nombre complexe non nul z, : arg ̅ = − arg
arg − = arg
+ < × 2+ M?.< ∈ Z
+ + + < × 2+ M?.< ∈ Z
Démonstration : z étant non nul, on peut l’exprimer sous forme trigonométrique : z = r (cos θ + i sin θ )
● Or, si z = r (cos θ + i sin θ ) , alors z = r cos θ − ir sin θ = r (cos θ − i sin θ ) = r (cos(−θ) + i sin(−θ))
On en déduit que ,: ̅ = − ,:
+ < × 2+ M?.< ∈ Z
,: − = ,:
+ + + < × 2+ M?.< ∈ Z .
● De z = r (cos θ + i sin θ ) , on déduit que −z = r (− cos θ − i sin θ ) , d’où
−z = r (cos(θ + π) + i sin(θ + π)) . On en déduit ,: −
=
,:
+ + + < × 2+ M?.< ∈ Z .
2. Arguments et opérations.
Théorème.
Pour tous nombres complexes non nuls z et z’, ,:
Preuve.
′ = arg
+ arg
+ < × 2+ M?.< ∈ Z
z et z’ étant non nuls, on peut les exprimer sous la forme trigonométrique :
z = r (cos θ + i sin θ ) et z ' = r ' (cos θ '+ i sin θ ') .
On a alors
zz ' = r (cos θ + i sin θ ) r ' (cos θ '+ i sin θ ')
= rr ' ((cos θ cos θ '− sin θ sin θ ') + i (cos θ sin θ '+ sin θ cos θ '))
zz ' = rr ' (cos(θ + θ ') + i sin(θ + θ ')).
On en déduit ,: ′ = arg
+ arg
+ < × 2+ M?.< ∈ Z .
Théorèmes.
Pour tous nombres complexes non nuls z et z’,
• Pourtoutentiernaturel@, ,: F = @ × ,:
J
• arg SHT = − arg
+ < × 2+ M?.< ∈ Z
H
• arg S H T = arg
+ < × 2+ M?.< ∈ Z
− arg ′ + < × 2+ M?.< ∈ Z
Démonstration.
• La première proposition se démontre par récurrence.
Pour n = 0. z étant un nombre complexe non nul,z V = 1? arg 1 = 0 + < × 2+ M?.< ∈ Z
La propriété est donc vraie au rang 0.
Soit p un entier naturel. Supposons que arg X = B × arg
+ < × 2+ , avec< ∈ Z.
X5J
X
On a alors : arg
= arg
+ arg
+ < × 2+ = B × arg
+ arg
+ < × 2+
arg X5J = B + 1 × arg
+ < × 2+
On a ainsi montré que pour tout B ∈ ℕ, si la proposition est vraie au rang p, elle est vraie au rang p+1.
La propriéré est vraie au rang 0 et elle est héréditaire. Elle est donc vraie pout tout @ ∈ ℕ.
7
● Démonstration de la deuxième proposition.

 1
1
z
J
0 = arg (1) = arg   = arg  z ×  = arg(z) + arg   . D’où arg SHT = − arg
z

 z
z
+ < × 2+ M?.< ∈ Z.
● Démonstration de la troisième proposition.
 z' 

 1
1
arg   = arg  z '×  = arg(z') + arg   = arg(z') - arg(z)
z

z
z
Interprétation géométrique de la différence.
Théorème.
Soient M et M’ les images respectives de deux nombres complexes distincts z et z’ dans le plan
r uuuuur
complexe.
Alors arg( z '− z) = (u; MM ') + k × 2π.
uuuuur
Preuve. Il suffit de remarquer que z’-z est l’affixe du vecteur MM ' .
Exercice. Soient z1 = 1 + i 3 et z2 = 1 + i .
1. Calculer le module et un argument de chacun des nombres complexes suivants :
2. Déterminer la forme algébrique de
z1 ; z2 ; z1 z2 et
z1
π
π
. En déduire les valeurs exactes de cos   et de sin   .


12 
12
z2
VIII. Notation exponentielle.
1. La fonction f : θ a cos θ + i sin θ
► Soit f la fonction définie sur ℝ par f (θ ) = cos θ + i sin θ .
► Soient θ et θ ' deux réels. On a alors f (θ + θ ') = f (θ ) × f (θ ') .
Donc la fonction f vérifie l’équation caractéristique de la fonction exponentielle.
►On admettra que l’on peut appliquer les règles de dérivation aux fonctions à valeurs dans ℂ.
La fonction f est alors dérivable sur ℝ et pour tout réel θ ,
f '(θ ) = − sin θ + i cos θ = i (i sin θ + cos θ ) = if (θ )
► On a donc f ' = if et f (0) = 1 .
Par analogie avec la fonction exponentielle, on adoptera la notation :
Notation :
Pour tout réel θ , on écrira ? Z[ = ./0* + 0 @*.
2. Règles de calcul.
Pour tous réels θ et θ ' et tout entier naturel n,
eiθ = e−iθ
; eiθ × eiθ ' = ei (θ +θ ')
n
; (eiθ ) = einθ (Formule de Moivre) ;
n
eiθ
= ei (θ−θ ')
iθ '
e
Remarques. La formule de Moivre s’écrit aussi : (cos θ + i sin θ ) = (cos nθ + i sin nθ )
eiθ = 1 et arg(eiθ ) = θ
8
z1
z2
.
3. Forme exponentielle d’un nombre complexe.
Théorème et définition.
Tout nombre complexe z non nul de module r et d’argument θ s’écrit : z = reiθ .
Cette écriture est une forme exponentielle de z.
Réciproquement, si z est un nombre complexe non nul s’écrivant z = reiθ , alors z = r et arg( z ) = θ
z Cz C
- z Bz A
Interprétation géométrique du module et d’un argument de
. (Méthode à retenir)
Soient A, B et C trois points deux-à-deux distincts du plan complexe d’affixes respectives z A , z B et zC .
On a alors :
z B - zC
z A - zC
z B - zC
=
z A - zC
H ]H
,: SH\ ]H^ T = arg
_
^
=
`
BC
AC
−
− ,:
a
b
−
a
= !" ; cd # -!"; ce#
= !"; cd # +!ce; "# = !ce; cd #.
H ]H
,: SH\ ]H^ T = !ce; cd #
_
^
Exercice 1.
r r
Dans le plan complexe muni d’un repère orthonormal direct (O, u , v ) , on considère les points A et B d’affixes
z+2
respectives (-2) et i , et pour tout z ≠ i les points M d’affixe z et M’ d’affixe z ' avec : z ' =
.
z −i
Déterminer :
a) l’ensemble (F) des points M du plan tels que M’ soit sur l’axe réel ;
b) l’ensemble (G) des points M du plan tels que M’ soit sur l’axe imaginaire.
c) l’ensemble (E) des points M du plan tels que OM’=1 ;
Corrigé.
z +2
est réel
z −i
Pour tout nombre complexe z ≠ i ,
 z +2
 z + 2 
z +2
 , < ∈ ℤ
= 0 ou arg 
=
k
×
π
est réel ⇔ 

 z − i 
 z − i

z −i
z +2
est réel ⇔ = −2/" ≠ −2? arg + 2 − arg − = < × +; < ∈ Z
z −i
= −2/" ≠ −2? arg + 2 − arg − = < × +; < ∈ Z
Pour tout nombre complexe z ≠ i , ! ≠ e? !"; e # − !" ; d # = < × +; < ∈ Z#
≠ −2? arg + 2 − arg − = < × +; < ∈ Z⇔ ! ≠ e? !" ; e # − !"; d # = <+; < ∈ Z#
≠ −2? arg + 2 − arg − = < × +; < ∈ Z⇔! ≠ e? !"; e # + !d ;"# = <+; < ∈ Z#
≠ −2? arg + 2 − arg − = < × +; < ∈ Z⇔! ≠ e? !d ; e # = <+; < ∈ Z#
On en déduit que : M’ est sur l’axe réel ⇔ M ∈ ( AB) − {B} . (F) est la droite (AB) privée du point B.
a) M’ est sur l’axe réel ⇔
b) M’ est sur l’axe des imaginaires ⇔
z +2
est imaginaire pur
z −i
Pour tout nombre complexe z ≠ i ,
 z +2
 z + 2  π
z +2

= 0 ou arg 
=
+
k
×
π
;
k
∈

est imaginaire pur ⇔ 

 z − i  2
 z − i

z −i
9


π
z +2
est imaginaire pur ⇔  z = −2 ou (z ≠ −2 et arg ( z + 2) − arg ( z − i ) = + k π; k ∈  )


z −i
2
r uuuur
r uuuur

 

 z ≠ −2 et arg ( z + 2) − arg ( z − i ) = π + k π; k ∈   ⇔  M ≠ A et u; AM − u; BM = π + k × π; k ∈  



 

2
2
r uuuur
uuuur r

 

 z ≠ −2 et arg ( z + 2) − arg ( z − i ) = π + k π; k ∈   ⇔  M ≠ A et u; AM + BM ; u = π + k π; k ∈  

 

2
2
uuuur uuuur

 

 z ≠ −2 et arg ( z + 2) − arg ( z − i ) = π + k π; k ∈   ⇔  M ≠ A et BM ; AM = π + k × π; k ∈  



 

2
2
(G) est le cercle de diamètre [AB] privé du point B.
c) OM’ = 1 ⇔
(
) (
)
(
) (
)
(
)
z +2
= 1 ; OM’ = 1 ⇔ ( z + 2 = z − i et z ≠ i) ;
z −i
OM’ = 1 ⇔ ( z + 2 = z − i ) car i + 2 ≠ i − i . Or z + 2 = AM et z − i = BM
Donc OM’ = 1 ⇔ AM = BM .
Ainsi, (E) est la médiatrice du segment [AB].
Exercice 2.
r r
Dans le plan complexe muni d’un repère orthonormal direct (O, u , v ) , on considère les points A et B d’affixes
z + 3i
respectives (- 3i ) et 4+i , et pour tout z ≠ 4 + i les points M d’affixe z et M’ d’affixe z ' avec : z ' =
.
z −4−i
1. Déterminer l’ensemble des points M tels que :
a) z ' soit réel ; b) z ' soit imaginaire pur.
2. Calculer le produit ( z '−1)( z − 4 − i ) .
En déduire l’ensemble des points M du plan tels que M’ soit un point du cercle de centre
C d’affixe 1 et de rayon 2 .
Corrigé partiel.
1. a) Avec la même méthode que l’exemple ci-dessus, on trouve la droite (AB) privée du point B.
b) On trouve le cercle de diamètre [AB] privé du point B.
 z + 3i

2. ( z '− 1)( z − 4 − i ) = 
− 1 ( z − 4 − i ) = z + 3i − ( z − 4 − i ) = z + 3i − z + 4 + i = 4 + 4i
 z − 4 − i 
M’ est un point du cercle de centre le point C d’affixe 1 est de rayon
2 signifie que z '− 1 = 2
Or, d’après l’égalité précédente, ( z '− 1) = 4 + 4i . Donc
z −4 −i
z '− 1 = 2 ⇔
4 + 4i
= 2
z − 4 − 4i
;
z '− 1 = 2 ⇔
4 + 4i
z − 4 − 4i
= 2


4 + 4i
z '− 1 = 2 ⇔  z − 4 − 4i =
et z ≠ 4 + 4i
2




Soit D le point du plan d’affixe 4 + 4i . Donc z '− 1 = 2 ⇔  MD = 4 2 et z ≠ 4 + 4i ⇔ ( MD = 4 et z ≠ 4 + 4i )


2

DB = 4 + i − (4 + 4i) = −3i = 3 . Donc z '−1 = 2 ⇔ MD = 4
On en déduit que l’ensemble des points cherché est la cercle de centre D et de rayon 4.
10