physique - unBlog.fr

Collège Classique de Bonabéri.
COLLEGE CLASSIQUE de BONABERI
Terminale C
PHYSIQUE
23 novembre 2007. Durée
Sujet proposé par Jean Jules FIFEN. Terminale C séquence 2 page 1 sur 4
: 3H30
EXERCICE 1 (7pts)
Cette exercice comporte deux parties indépendantes A et B.
Partie A 2,5pts
La comète Honda-Mrkos-Pajdusakoa passe à son périhélie le soir de Noël 1995, à 22h 17min 39s.
La figure1 en annexe, où S désigne le soleil, présente les positions de la comète tous les dix jours, avant
et après son passage au périhélie.
1. Sur la figure 1, placer le périhélie P et l’aphélie A de la trajectoire.
2. Rappeler les formules d’approximations des vecteurs vitesses et accélérations
3. Construire le vecteur vitesse de la comète à son passage au point P .
4
4. Construire le vecteur accélération de la comète à son passage au périhélie.
5. Déterminer le module de l’accélération de la comète à son passage au périhélie.
6. En déduire une valeur approchée de la masse du Soleil.
Données :
Echelle des vitesses :
.
61
1cm 10 m s− ≡
Echelle des accélérations :
.2 1cm 10m s
−
≡
Echelle de la figure :
,.1cm 0 25 U A≡.
U A 1 49 10 m=×Unité astronomique : 1 . .. , 11
Partie B 4,5pts
La figure 2 représente une poulie à deux gorges de rayons respectifs r01m,
1
=
et . Sur la
poulie est fixée une tige de longueur l dont le milieu coïncide avec le centre de rotation de la poulie. Sur
les gorges des poulies s’enroulent des câbles inextensibles et de masses négligeables aux extrémités
desquels sont fixés les solides (S
,
2
r03m=
) et (S ) de masses respectives 1 m3kg
=
et .
2
m4kg=
1 2
A l’instant initial, on abandonne le système sans vitesse initiale.
Le moment d’inertie du système { poulie + tige} est . Les frottements sur le sol sont
équivalentes à une force unique d’intensité
,.
2
0
J05kgm=
. On donne . 30 β =D
f
4N
=
β
(S1)
(S2)
Figure 2
1. Quelles sont les conséquences physiques directes de l’inextensibilité des câbles et de la négligence de
leurs masses ? 0,5pt
2. Représenter toutes les forces appliquées sur toutes les parties du système formé. 1pt
). 1,25pt 3. Déterminer les accélérations a et a prises respectivement par les solides (S ) et (S
1 2 1 2
) et de la poulie. 0,5pt
4. En déduire la nature des mouvements respectifs des solides (S ) , (S
1 2
) et de la poulie. 0,5pt 5. Ecrire les équations horaires du mouvement de (S1
6. Maintenant, la piste est verglacée (absence de frottement) et le plan sur lequel se déplace le solide
(S ) est relevé si bien que . 90 β =D
1

Collège Classique de Bonabéri.
Sujet proposé par Jean Jules FIFEN. Terminale C séquence 2 page 2 sur 4
). 0,25pt 6.1. En déduire les nouvelles accélérations prises par les solides (S ) et (S
1 2
des câbles. 0,25pt
6.2. En déduire les tensions T et T
1 2
6.3. Déterminer l’accélération du solide (S2) lorsqu’on fixe aux extrémités de la tige deux masses
ponctuelles identiques de valeurs m50g
=
0,25pt
EXERCICE 2 Le joueur de tennis (3pts)
On considère une balle de tennis de rayon ,r350cm
=
. Un joueur de tennis, situé dans la partie I du
court, tente de lober son adversaire (faire passer la balle au-dessus de ce dernier). Celui-ci est situé à
une distance derrière le filet, dans la partie II du court, juste en face du joueur. Le joueur
frappe la balle alors que le centre d’inertie de celle-ci est en A, à la distance D=9,00 m du filet et à la
hauteur au dessus du sol supposé parfaitement horizontal. La balle part alors avec une vitesse
initiale ( ) incliné d’un angle par rapport au sol, dans le plan perpendiculaire
au filet (plan de la figure 3).
,d200m=
,h050m=
0
V
G,.
1
0
V1200ms
−
=60 α =D
1. Etablir dans le repère (O, ,
i
G
j
G
α
0
V
G
A
O i
G
j
G
h
H
Partie II
Partie I
D
L L
d
f
ile
t
F
i
g
ure 3
), l’équation littérale de la trajectoire du centre d’inertie de la balle,
après le choc sur la raquette. 0,75 pt
2. En utilisant les valeurs numériques du texte, écrire l’équation de la trajectoire du centre d’inertie de
la balle. 0,25 pt
3. L’adversaire tient sa raquette à bout de bras et en sautant, elle atteint au maximum la hauteur
,
H
250m=par rapport au sol.
3.1. Peut-il intercepter la balle ? 1 pt
3.2. Quelle distance sépare alors la balle et l’extrémité supérieure de la raquette ? 0,25 pt
4. La ligne de fond étant à la distance ,
L
120m
=
du filet, la balle peut-elle retomber dans la surface de
jeu ? (autrement dit, le lob est-il réussi ?). 0,75 pt
EXERCICE 3 Mouvement d’un projectile. 3pts
On lance un projectile M, supposé ponctuel, de masse m, suivant une piste dont la figure4 représente la
trace ABC dans le plan vertical. . AB est horizontal, BC est circulaire, de rayon
OB OC r== ,r08m
=
,
tangente en B à AB. La longueur de la piste circulaire est le sixième d’une circonférence de même rayon.
Les frottements ainsi que la résistance de l’air sont négligeables. .2 g10ms
−
=
B
i
G
C
l
r
r
O
Figure 4
A A’ D
j
G
B

Collège Classique de Bonabéri.
Le lancement est effectué en faisant agir sur M initialement au repos en A, une force , horizontale,
d’intensité constante, sur une longueur . F
G
',lAA05m==
Sujet proposé par Jean Jules FIFEN. Terminale C séquence 2 page 3 sur 4
1. Déterminer la vitesse du projectile au point C, en fonction de F, m, r, l, g et
α
. 0,75 pt
C
V
2. Quelle doit être la valeur minimale de F pour que le projectile atteigne le point C ? 0,5 pt
3. On suppose que la force a pour intensité 2,0N. quelles est dans le repère (C, ,F
G
j
G
i
G) l’équation de la
trajectoire du projectile quand il a quitté C ? 1 pt
4. Déterminer la distance au point B du point d’impact D sur le plan horizontal contenant AB. 0,75 pt
EXERCICE 4 La verrière 3pts
L’élève KAPTUE de Terminale C lâche une balle de tennis sans vitesse initiale de sa fenêtre située à une
hauteur au dessus de la verrière oblique d’un magasin (voir figure 5). La balle rebondit sur la
verrière en un point A symétriquement par rapport à la normale à la verrière en ce point, sans
changement de valeur de sa vitesse. Elle atteint le sol en un point B à 9,0 m sous la fenêtre de KAPTUE et
à 12,0 m du pied du mur de l’immeuble.
,h60m=
1. Montrer que le mouvement de la balle est plan. 0,5 pt
2. Déterminer l’équation de la trajectoire de la balle. 0,25 pt
3. Quelle est l’angle de la verrière avec le plan horizontal ? 1 pt
4. Déterminer l’énergie cinétique de la balle en A et en B. 0,5 pt
5. Déterminer la hauteur maximale atteinte au-dessus du sol après rebondissement. 0,75 pt
La balle sera assimilée à un point matériel de masse ,m570g
=
.
EXERCICE 5 Mouvement parabolique d’un palet sur un plan incliné. 4 pts
Un palet est mis en mouvement sur une table à coussin d’air incliné d’un angle sur le plan
horizontal (voir figure 6). A l’instant initial t60
β =D
0s
=
,son centre d’inertie G est au point O, origine du
repère (O, ,
i
G
j
G). On le lance vers le haut et dans le plan de la table. Le vecteur vitesse initiale, 0
V
G
est
dans le plan incliné et fait un angle avec la direction horizontale (voir figure 5). La valeur de
l’accélération au lieu est . 45
α =D
,.
2
g980ms
−
=
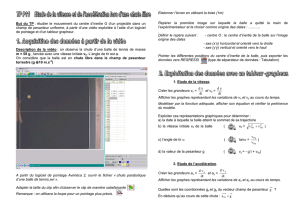
Un ordinateur relié à la table et à une imprimante enregistre les positions successives occupées par le
centre d’inertie G du palet, à des intervalles de temps réguliers de durée 50ms
τ
=
. L’impression de ces
positions à l’échelle 1/10 est donnée par la figure 7.
,D120m
=
A
B
,h60m
=
,d30m
=
Figure 5

Collège Classique de Bonabéri.
1. Repérer les coordonnées (x , y
i i) de chaque position occupée par le centre d’inertie du palet et calculer
les termes et , représentant respectivement les espaces parcourus suivant
l’axe (ox) et suivant l’axe (oy) pendant les intervalles de temps de durée
ii1
ax x
+
=−
iiii1
by y
+
=−
50ms
τ
=
. 1pt
x(m)
i
y(m)
i
a(m)
i
b(m)
i
0
V
G
e
a
G
2. On veut déterminer les modules de la vitesse initiale et de l’accélération expérimentale du
mouvement du palet.
2.1. Montrer à partir des termes et obtenus dans le tableau que le mouvement du palet est
uniforme suivant l’axe (ox) et uniformément varié suivant l’axe (oy). 0,5 pt
i
ai b
2.2. Déterminer le module de la vitesse initiale et de l’accélération expérimentale du
mouvement du palet.
0,75 pt
0
Ve a
2.3. En appliquant le théorème du centre d’inertie au mouvement du palet sur la table, dans
l’hypothèse où les forces de frottement sont négligeables, exprimer le module du vecteur
accélération théorique en fonction de g et . Faire l’application numérique. 1pt
th
a
β
2.4. Montrer que l’hypothèse des forces de frottement négligeables est acceptable. 0,5 pt
3. Ecrire l’équation de la trajectoire du palet et justifier la courbe obtenue à la figure 7. 0,5 pt
Sujet proposé par Jean Jules FIFEN. Terminale C séquence 2 page 4 sur 4