Cours de Macroéconomie

PARTIE 1 : UNE INTRODUCTION AUX MODÈLES DE CROISSANCE : LA DYNAMIQUE DE LONG
TERME
CHAPITRE 1 : Pourquoi s'intéresser à la croissance économique ?
1-1 Quelques faits stylisés sur la croissances et les revenus par tête dans le monde.
A - Les pays ont des revenus par tête différents.
Comment a évolué la distribution des PIB par tête depuis la période de l'après guerre ?
Aujourd'hui il y a des écarts très important entre les pays riches et les pays pauvres, à tel
point que l'on peut considérer que les pays les plus riches ont un niveau de vie 30 fois plus
élevé que les pays les plus pauvres.
Exemple : En moyenne le PIB / hab et de 34 000 $, au Méxique c'est 8 000 $, en Chine c'est 4
000 $, en Inde 2 500 $, Nigéria 1 000 $, Tchad < 500 $.
* Commentaire de courbe ( figure 1 ) : représentation de la distribution des revenus par tête
avec des grandes périodes dans le temps
- En 1960 : 15 ans après la fin de la 2nd guerre mondiale, la plupart des pays avaient un
revenu/personne < 1500 $
- En 1980 et 2000 : Le mode de la distribution se déplace vers la droite. Tous les 20 ans, le PIB
/ personne augmente. ( en 1980 le mode se situe environ à 3000 $ // en revanche nous
remarquons que la dispersion entre les deux courbes est beaucoup plus forte ). Alors même
que le revenu par tête augmente tous les 20 ans, la distribution des revenus devient plus
inégalitaire. En particulier, on a une concentration plus élevée de pays à l'extrémité droite
des distributions.
- Phénomène de stratification.
Il traduit le fait que dans l'évolution de la distribution des revenus, certains pays
s'enrichissent ; d'autres s'appauvrissent, ce qui signifie qu'on à de moins en moins de pays
au milieu de la distribution. La distribution des revenus par tête a tendance a devenir plus
symétrique
- La distribution du PIB par travailleur.
On pense que la richesse d'un pays est liée à sa capacité de productivité. On s'intéresse alors
à la richesse produite par chaque travailleur.
Cours n°1
04/09/2012
Macroéconomie

Lorsque l'on regarde la distribution des PIB / Travailleur au lieu de la distribution par tête les
conclusions sont identiques, c'est à dire que non seulement les inégalités s'accroissent dans
le temps mais on observe également une concentration plus forte du côté des pays les plus
riches. Il semble que le niveau de vie des pays soit associé à la capacité productive de ses
travailleurs. Il n'est pas impossible que le niveau de vie des pays soit directement tributaire
de la productivité du travail.
B - Croissance et bien-être économique.
Pourquoi le niveau revenu par tête n'est-il pas un indicateur suffisant pour mesurer le
"bonheur" des hommes ?
Dans les pays qui ont le niveau de vie le plus élevé, ont s'aperçoit que le PIB par tête est
corrélé avec d'autres indicateurs ( La consommation par tête et l'espérance de vie à la
naissance ). Les pays les plus riches sont également ceux ou la consommation par tête est la
plus élevée. On observe une corrélation entre le PIB/HAB et l'espérance de vie à la
naissance. C'est à dire que ceux ou le PIB/HAB est le plus fort, l'espérance de vie à la
naissance est la plus forte ( 80 ans pour les pays les plus riches, alors que dans les pays les
plus pauvres l'espérance de vie est comprise entre 40 et 50 ans ).
Bien qu'il existe une corrélation positive entre ces deux indicateurs, la causalité peut être à
double sens.
- La croissance a ses gagnants et ses perdants ( Schumpeter, Kuznets et les historiens )
On peut envisager que la capacité productive d'une économie repose sur un phénomène dit
de destruction créatrice. Cela signifie que le niveau de vie et la croissance à long terme d'une
économie repose des innovations majeurs. Certaines entreprissent disparaissent alors que
d'autre émergent. Cela entraine souvent des tensions sociales. Les historiens considèrent
que les institutions déterminent la croissance économique d'un pays.
L'approche historique met l'accent sur le lien entre la croissance et les institutions. Par
institution il faut comprendre la manière dont sont régenté les relations entre individus. Ces
relations sont nécessairement conflictuelles et expliquent qu'une hausse du niveau de vie
pour tous ne soit pas nécessairement souhaitée par toutes les composantes de la société.
C - Les pays les plus riches ont-ils les taux de croissance les plus élevés ?
Il semble que pour être riche, deux conditions doivent être réalisées : avoir une croissance
régulière, ce qui signifie que d'une année sur l'autre l'accroissement du PIB par tête est
proportionnel ( E.U & R U sur le graphique. ) De plus pour fermer le GAP, avec les pays les
plus riches la croissance doit être non seulement régulière mais beaucoup plus rapide, c'est
le cas par exemple des NPI ( nouveau pays riche ) ou bien de certains pays à revenu
intermédiaire comme le Boswanna.
De plus, certains pays peuvent se retrouver dans ce qu'on appelle un piège à pauvreté soit

parce que la croissance est irrégulière soit parce quelle est régulière mais pas assez forte.
D - De quelles périodes datent les différences que nous observons aujourd'hui entre les pays ?
Que montrent les données historiques depuis le milieu de XIXème siècle ?
Jusqu'en 1870 tous les pays du monde avaient un PIB / tête en dessous en de 500 $ et les
écarts de niveau de vie resté faible, en particulier, certaine grande civilisation comme la
Grêce, Rome, Chine… N'avaient pas de pib/tête très supérieur à celui des autres pays du
monde. La grande différence apparait au début du XIXème siècle où l'on voit un écart se
creser entre ceux qui bénéficient de la révolution industrielle et les autres. La révolution
industrielle transforme les structures productives et permet à ces pays d'avoir un taux de
croissance stable à long terme. On considère que c'est depuis cette période que datent les
écarts de richesse observé entre les pays.
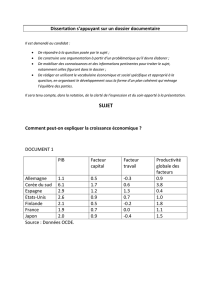
### EXAMEN COMMENTAIRE DE TABLEAU ET DE COURBE
DEUX PROBLÈMES À RÉSOUDRE ####
Quand on se situe avant la révolution industrielle, ce qu’on observe c’est que tous lesp ays on a peut
près le meme PIB par tête et croisse à des taux qui sontà peu près comparable. Ceci-ci est illustré par
Fig 1.11.
Manifestement, à partir du XIXème siècle, on constate une phase de décollage (ROSTOW).
E. La convergence conditionnelle
.Commentaires de l’équation de Barro
Les modèles de croissances ont deux objectifs : essayer de comprendre les causes de croissance d’un
pays et en tirer des recommandations pour les pays les plus pauvres puissent rejoindre le niveau des
pays les plus riches.
En d’autres termes, on veut comprendre comment la croissance peut faire converger les niveaux de
vie. Dans l’analyse de la croissance : on distigue deux types de converges : la béta convergence et la
sigma convergence.
LA BETA CONVERGENCE
On considère une année donnée, deux pays qui ont des niveaux de PIB par tête différent. Pour qu’il y
est convergence il faut que le plus pauvre ait un taux de croissance plus rapide que le plus riche. La
beta convergence traduit alors l’idée selon laquelle le taux de croissance d’un pays est d’autant plus
fort que son niveau de vie initiale (PIB par tête) est faible.
On distingue deux types de béta convergence :
La béta convergence absolue
La béta convergence conditionnelle
Cours n°2
11/09/2012

LA BETA CONVERGENCE ABSOLU
On veut savoir si deux pays qui ont les mêmes caractéristiques économiques mais des niveaux de vie
initialement différent convergent ou non.
LA BETA CONVERGENCE CONDITIONNELLE
La convergence des niveaux de vie n’est pas indépendante des caractéristiques de chaque pays
(institution politique, culture, politique économique, taux d’investissement…). La conséquence c’est
que un pays peut avoir un taux de croissance supérieur aux autres sans pour autant rattraper leur
niveau de vie.
La modification de la structure économique d’un pays en développement peut l’amener à se
rapprocher du niveau de vie d’un pays très développer (Etats Unis).
L’EQUATION DE BARRO
(Equation)
G correspond au taux de croissance d’un pays i entre deux années t-1 et t. y correspond au PIB par
tête du pays l’année t-1. X représente toutes les caractéristiques propres au pays i l’année t-1.
Epsylone représente toutt les facteurs de la croissance quie ne sont pas tenu en compte ici. Alpha et
Bétaa sont des paramètres.
Quand on s’intéresse à la convergence absolu, béta = 0 (on ne tient pas compte des caractéristiques
propres de chaques pays). Si béta différent de 0, alors on va avoir de la convergence ou de la
divergence conditionnelle.
Pour qu’il y est convergence, il faut que alpha soit négatif. Si alpha est positif ou nul, on dit qu’il n’y a
pas convergence dans le cas ou il est nul et il y a divergence dans le cas ou c’est positif.
Figure 1.14
Ce graphique illustre la convergence absolu. La droite rerprésente l’équation de barro quand alpha =
0.
Section 2 : Comptabilité de la croissance et régressions des taux de croissance
Décomposition ex-post des différents facteurs de productions.
Dans un premier temps, on va regrouper tous ce qui n’est pas du capital et travail dans un groupe
appelé progrès technique.
(1) : Q = (Q/NH) x NH
N représente les effectifs employés et H la durée moyenne du travail par personne employée.
Par conséquent Q/NH représente la production horaire du travail. La croissance d’un pays y est liée.
(2) : Taux de croissance dQ/Q = q = [ q – (n + h ) ] + (n + h) ; n = dN/N ; h = dH/H
n = taux de croissance des effectifs employés
h = taux de croissance de la durée moyenne du travail par personne employée
La croissance dans un pays va pouvoir être décomposé en deux, elle va dépendre de la croissance, de
la productivité horaire du travail et de la croissance du nombre d’heures travaillé.

Fonction de production macroéconomique (Cobb – Douglas) :
Q = L^a K^1-a PGF
L = NH heures travaillé ; K = Stock de capital ; PGF = Productivité global des facteurs (progrès
technique) et a = part du travail dans les facteurs de productions. 1-a = Part du capital.
En termes de taux de croissance : q = a x l + (1-a) k + pgf ; l= dL/L ; k = dK/K et pgf = dPGF/PGF
En outre, Q/L = (K/L)^(1-a)PGF
Taux de croissance de (Q/L) :
q-l = (1-a) (k-l) + pgf
Le taux de croissance de la productivité du travail dépend de la part de capital dans les facteurs de
production ( 1 – a), ça dépend aussi du travail de croissance de stock de capital en d’autres termes
l’investissement, du taux de croissance du nombre d’heures travaillés et enfin du taux de croissance
de la productivité global des facteurs.
q= [q – (n+h)] + (n+h)
Ces deux relations montrent que la croissance dans un pays sera d’autant plus importante que le
nombre d’heure travaillé augmentera et que la productivité du travail progressera à un rythme
élevée. Or, la croissance de la productivité du travail dépend elle-même de la croissance du stock de
capitale et de la croissance de la productivité global des facteurs, c’est-à-dire du progrès technique.
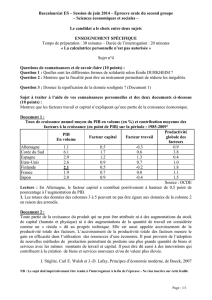
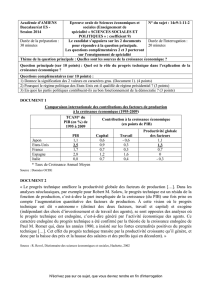
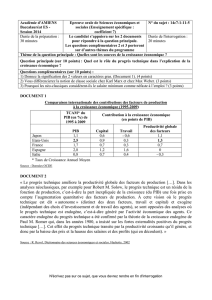
A. Outils de mesure des contributions de la croissance
Pas de consensus sur le rôle du capital et de l’éducation
On sait d’après les équations de décomposition de la croissance que celle-ci dépend du rythme
auquel un pays accumule du capital mais également du rythme auquel progresse de manière
indépendante la productivité du travail.
Polémique sur :
Comment mesurer l’investissement ?
Certains considère qu’il faut prendre en compte le taux d’investissement c’est-à-dire la part de
l’investissement dans le PIB. D’autres considère qu’il suffit de tenir compte du taux de croissance de
l’accumulation du capital. Mais tout le monde s’accorde sur un point, c’est que c’est bien
l’accumulation du capital qui semble avoir jouer un rôle pour expliquer la croissance des pays depuis
la fin de la 2nd GM.
Schéma croissance :
1. La contribution du capital au taux de croissance d’une économie est d’autant plus forte que ce
pays a initialement un niveau de vie minimum. Dans le tableau 1, ceci explique la différence de
comportement que l’on observe entre d’un coté les pays pauvres du continent latino-américain ou
africains et de l’autre, les économies en transitions ou industrialisées.
2. La productivité des facteurs égale à celui du capital notamment dans les économies en phase de
rattrapage. Ex : Chine ou pays asie de l’est. Alors que son effet est minoré dans les pays pauvre.