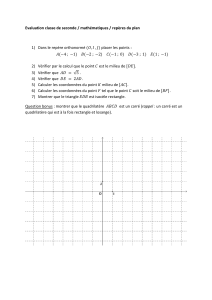
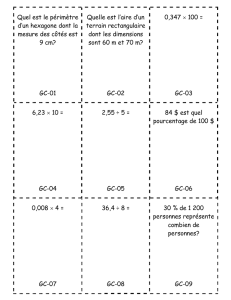
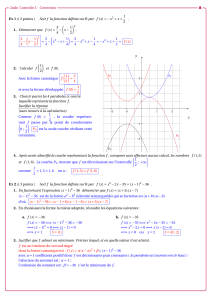
Irrationalité de /2 - Page personnelle de Baptiste GORIN

Irrationalité de
√
2
Baptiste GORIN
√
Théorème. — 2 est irrationel.
Démonstration
√
Première démonstration. — Supposons par l’absurde que 2 est un nombre rationnel. Il existe alors p, q ∈ N∗
√
p
premiers entre eux tels que 2 = . Alors p2 = 2q 2 . Par suite, p est divisible par 2 : p = 2p′ . Donc 2p′2 = q 2 .
q
q est alors également divisible par 2. On aboutit à une contradiction.
√
Deuxième démonstration. — Supposons par l’absurde que 2 est un nombre rationnel. Il existe alors p, q ∈ N∗
√
p
tels que 2 = . Alors p2 = 2q 2 . En considérant les décompositions en facteurs premiers de p et q, on constate
q
que p2 et q 2 ont un nombre pair de facteurs premiers. Comme 2q 2 a un nombre impair de facteurs premiers, on
aboutit à une contradiction.
√
∗
est un nombre
Troisième démonstration.
— Supposons par l’absurde que
√
√ 2 √
√ rationnel. Il existe alors m ∈ N ,
minimal, tel que m 2 soit un entier. Considérons n = m( 2 − 2 ) = m( 2 − 1). Notons que n est un nombre
√
√
entier tel que 0 6√n < m.
√ De
plus n 2 = 2m − m 2 est un entier. Le caractère minimal de m assure alors que
2 = 1. On aboutit à une absurdité.
n = 0. Par suite 2 =
Quatrième démonstration. — Par le théorème de Pythagore, un triangle rectangle isocèle dont les côtés de l’angle
√
√
√
p
droit ont pour longueur 1 a une hypoténuse égale à 2. Donc, si 2 est rationnel, avec 2 = , p, q ∈ N∗ ,
q
l’image d’un tel triangle rectangle par une homothétie de rapport q est un triangle rectangle isocèle dont les
longueurs des trois côtés sont des nombres entiers. Par suite, il doit exister un plus petit triangle rectangle
isocèle ayant cette propriété. Mais, à l’intérieur d’un triangle rectangle isocèle dont les longueurs des côtés sont
des nombres entiers, on peut toujours construire un plus petit triangle ayant les mêmes propriétés :
√
Par suite, 2 ne peut pas être rationnel.
√
Cinquième démonstration. — Supposons par l’absurde que 2 est un nombre rationnel. Il existe alors p, q ∈ N∗ ,
√
p
avec q minimal, tels que 2 = . On a p > q et q > p − q. De plus :
q
p
√
2−
2q − p
2− 2 √
q
=√
= 2
= p
p−q
2−1
−1
q
Ceci contredit le caractère minimal de q.
√
Sixième démonstration. — Considérons l’ensemble E = {a + b 2; a, b ∈ Z}. E est fermé et stable pour l’addition
et la multiplication.
√
√
Considérons α = 2 − 1 ∈ E. Pour tout n ∈ N, αn ∈ E de sorte qu’il existe an , bn ∈ Z tels que αn = an + bn 2.
√
√
p
Si 2 est rationnel, il existe alors p, q ∈ N∗ tels que 2 = . D’où :
q
√
1
an q + b n p
αn = an + bn 2 =
>
q
q
Or, comme α ∈]0; 1[, on a lim αn = 0. On aboutit à une contradiction.
n→+∞
√
Septième démonstration. — Supposons par l’absurde que 2 est un nombre rationnel. Il existe alors p, q ∈ N∗
√
p
premiers entre eux tels que 2 = .
q
√ n
Alors 2 q est un nombre entier pour tout n ∈ N. En effet
n
√ n
2 2 q si n est pair
n−1
2 q=
2 2 p si n est impair
Irrationnalité de
√
2
On en déduit que
n X
√ k
√
n
n
( 2 − 1) q =
(−1)n−k 2 q ∈ N∗
k
k=0
Or, comme
pour tout n ∈ N.
√
√
2 − 1 ∈]0; 1[, on a lim ( 2 − 1)n q = 0.
n→+∞
On aboutit à une contradiction.
√
Huitième démonstration. — Supposons par l’absurde que 2 est un nombre rationnel. Il existe alors p, q ∈ N∗
√
p
avec q minimal tels que 2 = .
q
Alors le carré de côté de p a la même aire que deux carrés de côté q.
=
+
Plaçons les deux carrés de côté q à l’intérieur du carré de côté p en deux sommets opposés. Trois carrés dont
les côtés sont entiers apparaissent.
Les deux carrés situés en deux sommets opposés sont égaux et la somme de leur aire est égale à l’air du troisième
carré.
=
+
Ceci contredit le caractère minimal de q.
C.Q.F.D.