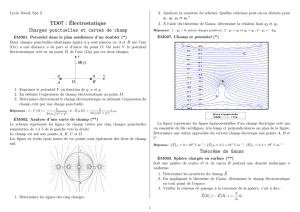
1 Problème : Champ électrostatique associé à l`atome d`hydrogène

◦
V( )
~
E=−−−→ V
+e
ρe
~ur
~
E( ) = E( ) ~ur
r
E(M)
r
~
E( ) = E( ) ~ur
V( ) = V( )
+e

~
E+( ) = e
4πε0r2~ur
V+( ) = e
4πε0r
α ρe
(β r)β
r
r r + dr
r ρe(r) (4πr2dr)
dq= 4πr2αexp [−β r] dr
λ(r)
λ(r)=4πr2αexp [−β r]
λ:r→λ(r)
dλ
dr= 4πα exp [−β r]2r−βr2
r=r0=2
β
Qe=−e
−e=ˆ∞
r=0
dq=ˆ∞
r=0
4πr2αexp [−β r] dr= 4πα 2
β3

−e= 8πα
β3
α β
r0
β=2
r0
α=−eβ3
8π=−e
πr3
0
ρer0
ρe=−e
πr3
0
exp −2r
r0
λ= 4πr2ρe
λ=−4er2
r3
0
exp −2r
r0=−e r02r r02
exp −2r
r0
λ r
x=2r
r0
λ:x−→ λ(x) = −e
r0x2exp(−x)
x1rr0λ(x)∼ − e
r0x2λ(x)
x= 0
λ(x)x= 2 r=r0
limx→∞λ(x) = 0
0
−e
r0
−2e
r0
−3e
r0
λ(x)
0 2 4 6 8 10
λ(x)x=r
r0
~
E−( ) = E−( ) ~urV−( ) = V−(r)

Σ
r
Φ = ‹Σ
~
E−·d~ S=Q(r)
ε0
Σ d~ S= dS ~ur~
E−=E−( ) ~ur
Φ
Φ = ‹Σ E−( ) dS= 4πr2E−( )
~
E−( ) = Q(r)
4πε0r2~urQ(r) = ˆr
u=0
λ(u)du
rr0
Q(r) = −4e
r3
0ˆr
u=0
u2exp −2u
r0du∼ −4e
r3
0ˆr
u=0
u2du=−e
62r r03
rr0~ E−( ) ∼ − e
3πε0
r
r3
0
~ur
rr0
Q(r)∼ −e
rr0~ E−( ) ∼ − e
4πε0r2~ur
~
E−(r=r0) = −e[1 −5 exp(−2)]
4πε0r2
0
~ur
E−(r=r0)∼ −16,6.1010 −1
r→0
limr→0E(r) = ∞limr→0V(r) = ∞
r→ ∞

limr→∞E(r) = 0 limr→∞V(r)=0
−e
r04πr2
0
σ0=−e
4πr2
0
r > r0r
r > r0~ E=~ 0V= 0
r < r0r
+e
r < r0~ E=e
4πε0r2~ur
r=r0
r0
0< r < r0ρ(r)=0
V r
∆
∆V=1
r2
d
drr2dV dr
0< r < r0
1
r2
d
drr2dV dr= 0
r2dV
dr=a⇒dV dr=a r2