DS 1 Physique-Chimie Problème 1 : Étude du mouvement d`un

M m
g= 9,81 −2
ex
y
ev
0
Oθ
0
g
m−→ v0θ0
−→
v0−→ v0=v0−→ u−→ u
−→
v(t)=(vx(t), vy(t)) −−→ OM(t)=(x(t), y(t))
O
vx(t)vy(t)
x(t)y(t)
tfv0g θ0
L0
L0=v2
0
gsin(2θ0)
L0
θ0
L0tfv0= 55 −1θ0= 52o
t0= 50 v0v∞
θ0
v0
v∞

R= 4 −→ v v
−→
F=−1
2ρSCxv2−→
u
ρ S R Cx−→ u
−→
v
Cx
Cx
ν= 1,5.10−5 2 −1
oρ= 1,2−3
−→
v(t) = v(t)−→ u
−→
v v
dv
dt +αv2= 0
α ρ R Cxm
α= 0.22 −1
v(t) = v0
1 + v0αt
x(t)y(t)v0α θ0
f:x→1
1 + ax F:x→1 aln(1 + ax)
t1
t1=1
αrαsin θ0 g−1 v0
v1t1
x1y1t1

t=t1
t2> t1y1
v1θ0g
t2x2y2
−→
v(t)t>t2
−→
v∞
α g
−→
v∞
−→
v∞
t3

0 1 2 3 4 5 6 7 8 9 10
1
0
1
2
3
4
5
6
7
8
8
1
2
3
4
0
10 20
30
40
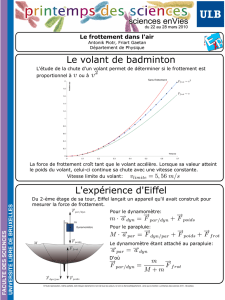
y(m)
x(m)
v = 55 m/s
0
θ= 52°
0v = 6.5 m/s
∞
Cx
Re
Re=Lv
ν
L v ν
(Re<1)
Re>1000

−→
g
g= 10 −2
˙x(t) = dx
dt ¨x(t) = d2x dt2
x(t) = Xmcos(ωt +ϕ)
x(t) = Xmejωt+ϕ=Xmejϕejωt =Xmejωt
x(t) = Re(x(t)) Xm=Xmejϕ Xmx(t)
Xm=|Xm|ϕ=Arg(Xm)
m= 1,0.103kg
k= 1,0.105−1l0
z(t) (Oz)
−→
uzz(t)
ze