Correction udPPC

Baccalauréat STI2D et STL
SPCL
Epreuve de sciences physiques
Correction
Session novembre 2015
Nouvelle Calédonie
20/11/2015
www.udppc.asso.fr

Si vous repérez une erreur, merci d’envoyer un message à : pa_besancon[at]udppc.asso.fr
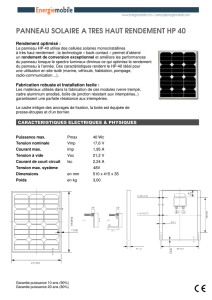
PARTIE A : le projet Stratobus
A.1. «...77 ans après la catastrophe du Hindenburg, le dirigeable, abandonné à
l'époque car trop dangereux, pourrait bien faire son grand retour dans le transport
d'hommes et de fret. » http://www.mobilite-
durable.org/
La tragédie du
Hindenburg le 6 mai
1937
Le zeppelin Hindenburg était-il gonflé à l'hélium ou au dihydrogène ? Justifier votre
réponse à l'aide du document 1 page 11.
D’après le document, seul le dihydrogène est inflammable (d’après les
pictogrammes) ; le Hindenburg était donc gonflé au dihydrogène.
A.2. Comme il est prévu que le Stratobus soit en vol stationnaire à 20 km
d'altitude et à une température stable, il pourra être gonflé avec du dihydrogène en
toute sécurité.
A.2.1. À l'aide du document 2 page 11, déterminer graphiquement la pression
atmosphérique P, la température T ainsi que la masse volumique de l'air ρair à
l'altitude prévue pour le Stratobus.
Voir courbe page suivante.
Le stratobus sera à 20 km d’altitude.
La courbe verte donne la pression : P = 5 kN/m2 = 5000 Pa (1 Pa = 1 N/m2)
La courbe orange donne la masse volumique : ρair = 0,09 kg/m3
La courbe rouge donne la température : T = 216 K

A.2.2. Convertir la température T obtenue en A.2.1. en degrés Celsius.
T(°C) = T(K) - 273,15 = 216 – 273,15 = - 57,15 °C
A.2.3. En vous aidant du texte de présentation 1 et de la question A.2.1, montrer
que la masse d'air mair déplacée par le Stratobus vaut mair = 4,5 t à une altitude de
20 km.
D’après le texte de présentation, le volume du stratobus est V = 50000 m3.
D’après la question A.2.1., la masse volumique de l’air à l’altitude de 20 km
est ρair = 0,09 kg/m3.
5 216
0,09

Donc la masse d’air déplacée est mair = ρair  V = 0,09  50000 = 4 500 kg
soit 4,5 t (1 t = 1000 kg)
A.2.4. Calculer alors l'intensité de la poussée d'Archimède FA (documents 3 et 4
page 12). Vous donnerez votre résultat en kilonewton (kN).
D’après les documents 3 et 4, on a :
FA = mair  g et g = 9,75 m.s–2 à 20 km d’altitude.
FA = mair  g = 4 500  9,75 = 43 875 N
Soit FA = 44 kN avec 2 chiffres significatifs.
A.2.5. Tracer sur le document réponse DR1 page 15 les vecteurs FA
⃗
⃗
⃗
⃗
et P
⃗
⃗
correspondant à la poussée d'Archimède et au poids du Stratobus lorsqu'il est en
position stationnaire. Vous préciserez l'échelle utilisée.
Le stratobus n’est soumis qu’à 2 forces : son poids et la poussée
d’Archimède. Il est en position stationnaire : donc ces deux forces se
compensent.
À l’échelle de 1 cm pour 20 kN, ces 2 vecteurs sont représentés par des
flèches de
44
20
= 2,2 cm.
Échelle – 1 cm pour 20 kN
Vue de face du
Stratobus avec son
centre de gravité G.
A.2.6. Le dihydrogène contenu dans le Stratobus aura une masse volumique
ρH2 = 7,0.10–3 kg.m–3 à cette altitude. Calculer la masse de dihydrogène mH2
contenue dans le Stratobus.
mH2 = ρH2  V = 7,0.10–3  50 000 = 350 kg
A.2.7. La masse du Stratobus se répartit entre le dihydrogène (mH2), l'équipement
de fonctionnement (mfonc) et la charge utile (mu). Exprimer le poids P du Stratobus
en fonction des diverses masses et de l'accélération de la pesanteur g.
P = mstratobus  g = (mH2 + mfonc + mu)  g
A.2.8. Le Stratobus devra transporter une masse utile mu = 300 kg. À l'aide de la
question A.2.7. et du document 4 page 12, déduire la masse de l'équipement de
fonctionnement mfonc du Stratobus. Vous donnerez votre résultat en tonnes (t).
FA
⃗
⃗
⃗
⃗
⃗
P
⃗
⃗

D’après le document 4 : g = 9,75 m.s–2.
D’après la question A.2.7. : (mH2 + mfonc + mu) =
P
g
=
44 000
9,75
= 4500 kg
Avec mH2 = 350 kg et mu = 300 kg, on trouve :
mfonc = 4500 – 350 – 300 = 3850 kg soit 3,85 t.
A.3. Le Stratobus devra rester stationnaire malgré des vents pouvant aller
jusqu'à 90 km.h–1.
A.3.1. Donner la vitesse maximale des vents vvent en mètres par seconde.
Vvent = 90 km.h–1 soit
90 1 000
3 600
= 25 m.s–1.
A.3.2. L'intensité de la force Fvent exercée par les vents sur le Stratobus est donnée
par la relation :
Fvent =
2
air x
1.ρ .S.C .v
2
ρair : masse volumique de l'air en kg.m-3
S : surface frontale du Stratobus en m2
Cx : coefficient de traînée sans unité
v : vitesse des vents en m.s–1
Calculer la force de résistance maximale de l'air Fvent qui s'exercerait sur le
Stratobus en vous aidant du texte de présentation 1, de la question A.2.1. et du
document 5 page 12. Vous donnerez votre résultat en kilonewton (kN).
On a : Fvent =
2
air x
1.ρ .S.C .v
2
D’après le texte de présentation S = π  R2 avec R =
34
2
= 17 m :
Donc S = π  172 = 908 m2