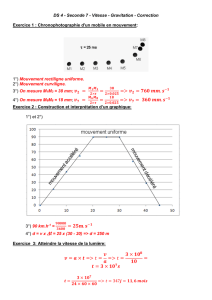
Orbite de la planète

1
TERMINALE S
PARTIE COMPRENDRE
MOUVEMENTS DES
SATELLITES ET DES
PLANETES
Mouvements de satellites et de planètes.
1) Lois de Kepler
Première loi de Kepler : toutes les orbites des planètes sont des ellipses
dont le soleil occupe l'un des foyers.
Seconde loi de Kepler: pendant des intervalles de temps t égaux la
planète balaye des surfaces 'S' égales de l'ellipse.
Schéma:
Si t = t1-t0= t3-t2 alors les surfaces sont égales S1=S2
Remarque : dans le cas d'une trajectoire circulaire le mouvement est uniforme
Troisième loi de Kepler ou loi des périodes:
Soit T la période de révolution de la planète autour du soleil, et 'a' la
longueur du demi-grand axe de l'ellipse.
La période de révolution au carré divisée par le demi-grand axe 'a' au cube
est une constante. La période T ne dépend pas de la planète mais
uniquement de la masse MS du soleil et de la constante d'attraction
universelle G :
S
M.G
2
π.4
3
a
2
T
Application
G = 6,67.10-11N.kg-2.m2 : constante de
gravitation universelle
MS = 1,96.1030 kg: masse du soleil.
Dans le cas particulier ou l'ellipse est un cercle, a = R (rayon de l'orbite
Soleil
S2
S1
Orbite de la
planète
t1
to
t3
t2
M
F
F'
O
2a
2b

2
circulaire). La période de révolution de la planète vaut:
S
3
3
S
2
2
S
2
3
2
M.G
R
.π.2T
R..
M.G
π.4
T
M.G
π.4
R
T
2) Mouvement circulaire uniforme
a- Repère de Frenet
Dans ce type de mouvement changent constamment de direction.
On détermine leurs composantes dans un repère
de Frenet, d’origine au centre d’inertie du corps
étudié et de vecteurs unitaires .
vecteur tangent au cercle dans le sens de
rotation, vecteur de direction perpendiculaire à
le trajectoire, et orienté vers son centre et
vecteur perpendiculaire aux deux premiers.
Dans ce repère
b- Accélération normale
Pour un mouvement circulaire uniforme v = Cte ( dv/dt = 0 ) et R = Cte, donc la
composante tangentielle de l’accélération est nulle et la composante normale
an = v2/R est constante. Dans un mouvement circulaire uniforme :
.
Dans un mouvement circulaire et uniforme
l’accélération est radiale ( de direction
correspondant au rayon du cercle) et centripète (
orientée vers le centre du cercle).
3) Nature du mouvement des satellites et des planètes
Les satellites et les planètes ne s’écrasent pas sur l’astre attracteur et ne s’en
éloignent pas non plus, donc le mouvement est circulaire et uniforme ( si sa vitesse
augmente, il s’éloigne et si elle diminue il se rapproche).

3
a- Force gravitationnelle
La force gravitationnelle exercée par l’astre attracteur est :. (
C’est une force radiale et centripète
G : constante gravitationnelle ( G = 6,67.10-11
N.m2.kg-2); M : masse de l’astre attracteur,
Terre pour les satellites et Soleil pour les
planètes (kg) ; m : masse du satellite ou de la
planète en orbite autour de l’axe attracteur (
kg) ; R : rayon de l’orbite du satellite ou de la
planète (m) ; vecteur unitaire orienté du
centre O de l’orbite vers le centre d’inertie du
corps en orbite.
b- Application de la 2° loi de Newton
, avec la force gravitationnelle, radiale et centripète,
c’est à dire orientée vers le centre de la trajectoire.
Donc l’accélération est radiale et centripète :
et la 2° loi de newton
s’écrit : .
c- Détermination de la vitesse
. Pour un satellite terrestre R = RT + h
d- Détermination de la période de rotation
Elle est notée T, c’est la durée de la longueur d = 2R à la vitesse v = (GM/R)1/2, soit
R : rayon de l’orbite ( m ); G : constante gravitationnelle (U.S.I);
M : masse de l’astre attracteur (kg).
(relation en accord avec la 3° loi de Kepler :
)
3° les satellites géostationnaires
Le satellite est géostationnaire s’il reste à la verticale d’un même lieu au dessus de la
Terre. Ce qui est possible à la verticale de l’équateur avec une période de rotation
égale à celle de la terre.

4