IFT 436 - Algorithmes et structures de données Algorithmes de base

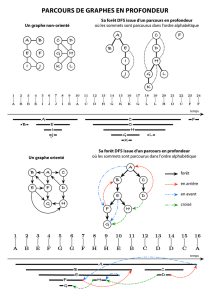
Parcours des graphes
IFT 436 - Algorithmes et structures de donn´ees
Algorithmes de base sur les Graphes
Rachid Kadouche
Universit´e de Sherbrooke
18 juillet 2013
1

Parcours des graphes
Parcours en largeur (BFS)
Parcours en profondeur (DFS)
Tri-Topologique
Algo BFS
Soit G= (S,A) et une racine s∈S.
BFS trouve tous les sommets atteignable `a partir de s.
Calcule la distance entre set les sommets.
Produit un Breadth-First-Tree (BFT) de racine s.
Algo fonctionne pour les graphes orient´e et non-orient´e.
2

Parcours des graphes
Parcours en largeur (BFS)
Parcours en profondeur (DFS)
Tri-Topologique
BFS : d´etails
Assume que nous utilisons une liste d’adjacence
Maintient 4 structures de donn´ees
color[u] : la couleur du sommet u∈S.
π[u] : le pr´ed´ecesseur de u.
d[u] : la distance entre set u.
Q: une liste FIFO pour g´erer les sommets gris.
3

Parcours des graphes
Parcours en largeur (BFS)
Parcours en profondeur (DFS)
Tri-Topologique
BFS - Pseudo
Algorithme : BFS(G, s)
1foreach u∈S− {s}do
2color[u] ←Blanc ; d[u] ← ∞ ;π[u]←NIL;
3color[s] ←Gris ; d[s] ←0 ; π[s]←NIL;
4Q← ∅ ; Enqueue(Q,s);
5while Q6=∅do
6u←Dequeue(Q);
7foreach v∈Adj[u]do
8if color[v] = Blanc then
9color[v] ←Gris ; d[v] ←d[u] + 1 ; π[v]←u;
10 Enqueue(Q,v);
11 color[u] ←Noir;
4

Parcours des graphes
Parcours en largeur (BFS)
Parcours en profondeur (DFS)
Tri-Topologique
Exemple BFS
5