TD: Haut-parleur

TD: Haut-parleur
1 Position du probl`eme Archim`ede. PC. 1998
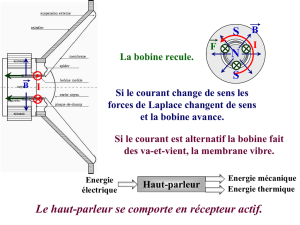
Un haut-parleur est constitu´e d’une bobine plate (b) d’axe z0z(de r´esistance R, d’inductance L, comportant
Nspires de rayon a) solidaire d’une membrane pouvant se d´eplacer parall`element `a elle-mˆeme, suivant la
direction z0znormale `a son plan. L’´equipage mobile (bobine + membrane) a pour masse totale m. Lorsque la
bobine s’´ecarte de sa position d’´equilibre d’un ´ecart alg´ebrique z, elle est rappel´ee par une force ´elastique due `a
un ressort de raideur k. De plus, l’air produit sur la membrane une force de frottement visqueux, proportionnelle
`a sa vitesse de d´eplacement, qui peut s’´ecrire: ~ f=−h.~v (avec h > 0).
La bobine est plac´ee dans un champ magn´etique uniforme
x
Bradial, normal `a z0z, cr´e´e par un aimant
permanent (A).
Pi`eces m´ecaniques: 1. saladier; 2. suspension externe; 3. membrane+cache poussi`ere; 4. spider
Pi`eces du moteur: 5. bobine mobile; 6. noyau; 7. aimant permanent (A); 8. entrefer; 9. plaque de champ
N
S
dl
bobinage
B
B
u
ur
km
bobine
membrane
N
S
SB
B
´
Etude du dispositif mobile: bobine - membrane
On applique aux bornes de (b) une tension variable u(t); la bobine est alors travers´ee par un courant
d’intensit´e i(t) et la membrane se d´eplace avec la vitesse instantan´ee v(t).
1. ´ Etude du haut-parleur
a. Exprimer la force de Laplace `a laquelle la bobine est soumise. (On d´esignera par `la longueur totale
du bobinage de (b) )
b. D´eterminer la force ´electromotrice ´el´ementaire, de, induite par le d´eplacement dz.~uzd’un ´el´ement
(a.dθ.~uθ) de bobine dans le champ B.~ur.´ Etendre le r´esultat `a la bobine tout enti`ere.
c. ´ Ecrire le th´eor`eme de la r´esultante cin´etique pour l’´equipage mobile (´eq. M), d’une part, puis l’´equation
´electrique relative au haut-parleur lorsqu’on applique une tension u(t) (´eq. E), d’autre part.
La tension appliqu´ee ´etant sinuso¨ıdale, de fr´equence f, on pourra ´ecrire u(t) = Um.cos(ω.t), avec ω= 2.π.f .
d. ´ Ecrire les deux relations (M’) et (E’) liant les expressions complexes ˜u(t) ,˜ı(t) et ˜v(t) associ´ees respec-
tivement `a u(t), i(t) et v(t).
e. ´ Eliminer la vitesse ˜v(t) entre les ´equations (M’) et (E’) pour faire apparaˆıtre une relation entre ˜u(t) et
˜ı(t)
f. L’imp´edance totale du dispositif est la somme de deux contributions: ˜ Z(ω) = ˜ Ze(ω) + ˜ Zm(ω). On
qualifie ces deux termes respectivement d’imp´edance propre et d’imp´edance motionnelle. Montrer que
l’imp´edance motionnelle ˜ Zm(ω) correspond `a l’association d’´el´ements comme Rm,Lmet Cmdont on
pr´ecisera la nature. Illustrer en repr´esentant le sch´ema ´electrique ´equivalent de l’imp´edance ˜ Z(ω).
2. ´ Etude du diagramme de Nyquist et de Bode.
1

ISEN-Brest. Kany. TD: Haut-parleur
a. On met Zm(ω) sous la forme R(ω) + j.S(ω). Tracer num´eriquement les fonctions R(ω) et S(ω).
b. V´erifier que, lorsque la pulsation varie de z´ero `a l’infini, le point M(ω) du plan complexe, d’affixe
˜
Zm(ω) d´ecrit un cercle (passant par les trois points d´etermin´es ci-dessus).
c. Pour quelle pulsation le module de l’imp´edance ˜ Zm(ω) est-il maximal ? Calculer || ˜ Zm(ω)||max.
d. Rechercher les pulsations ω1et ω2telles que || ˜ Zm(ω)|| soit ´egal `a 1
√2.|| ˜
Zm(ω)||max. Calculer le facteur
de qualit´e: ω0
ω2−ω1.
3. Bande passante acoustique.
Par analogie avec une r´esistance ´electrique, on peut introduire une r´esistance acoustique Rad´efinie `a partir
de la puissance acoustique Papar la relation: Pa=Ra.hv2i=1
2.Ra.(v.v∗), vd´esignant la vitesse de
d´eplacement du syst`eme bobine-membrane.
a. En utilisant les relations (M’) et (E’), ´etablir le rapport ˜v(t)
˜u(t)(on n´egligera le terme L.ω). Sachant
que la tension d’alimentation de la bobine a toujours une amplitude constante Umet une pulsation
variable ω, ´ecrire l’expression de ˜v(ω).
b. D´eterminer la quantit´e: hv2i=1
2.(v.v∗) en fonction de la pulsation ω.
c. ´ Etudier la variation de loghv2ien fonction de log ω(comparable au diagramme de Bode).
La r´esistance acoustique Rad´epend du rayon de courbure ρde la membrane. En d´esignant par cla c´el´erit´e
du son dans l’air, on peut montrer que:
* si ω < c
ρ=ωc,Raest proportionnelle `a ω2,
* si ω > c
ρ,Rademeure sensiblement constante.
d. Tracer le diagramme du type log(Ra) en fonction de log ω.
e. En d´eduire le diagramme relatif `a la puissance Pa, traduisant la variation de log Paen fonction de
log ω. Montrer que cette puissance demeure pratiquement constante dans une gamme de pulsation (ou
de fr´equence) que l’on pr´ecisera.
Donn´ees num´eriques:
Champ magn´etique B= 0,8 T
Rayon de la bobine a= 5 mm
Nombre de spires N= 160
Raideur du ressort k= 1425 N.m−1
Coefficient de frottement h= 0,28 N.s.m−1
Masse de l’´equipage mobile m= 100 mg
R´esistance de la bobine R= 630 Ω
Inductance de la bobine L= 1 mH
C´el´erit´e du son c= 340 m.s−1
Rayon de la membrane ρ= 1,6 cm
Solution
1. a. ~
F=RI.−→ d`∧
x
B=−I.`.B.~uz
b. Rde.I =−F. dz
dt= +I.`.B. dz dt⇒e= +`.B. dz dt
(ou bien en ´ecrivant: de= (~v ∧
x
B).−→ d`=dz
dt.B.a.dθ⇒e=dz dt.B.`).
c. D’apr`es le principe fondamental de la dynamique, on a: m. d2z
dt2=−k.z −I.`.B −h. dz dt
⇒d2z
dt2+h m.dz dt+k m.z =−I.`.B m(M)
D’apr`es la loi des mailles: u(t) + einduit =R.I +L. dI
dt⇒L. dI dt+R.I −`.B. dz dt=u(E)
d. Pour l’´equation m´ecanique, on a: (−ω2+j.ω. h
m+k m).˜z=−˜
I.`.B
m
ou bien: (j.ω +h
m+k m.j.ω ).˜v=−˜
I.`.B
m(M’)
Pour l’´equation ´electrique, on a: (j.ω.L +R).˜ I= ˜u+`.B.˜v(E’)
e. ˜v=−˜
I.`.B
j.ω.m+h+k
j.ω
d’apr`es (M’)
On peut r´e´ecrire (j.ω.L +R).˜ I= ˜u+`.B.˜vsous la forme: j.ω.L +R+`2.B2
j.ω.m+h+k
j.ω .˜
I= ˜u.
2

ISEN-Brest. Kany. TD: Haut-parleur
⇒˜u=j.ω.L +R+1
j.ω. m
`2.B2+h `2.B2+k j.ω.`2.B2.˜
I.
f. ˜ Ze=R+j.ω.L et 1
˜
Zm=j.ω. m
`2.B2+h `2.B2+k j.ω.`2.B2=1 ZCm+1 Rm+1 ZLmrepr´esente l’association
d’une r´esistance Rm, d’une inductance Lmet d’une capacit´e Cmen parall`ele.
On pose: Rm=`2.B2
h;Lm=`2.B2 ket Cm=m `2.B2
3. a. D’apr`es (M’): (j.ω +h
m+k m.j.ω ).˜v=−˜
I.`.B
m
D’apr`es (E’): (j.ω.L +R).˜ I= ˜u+`.B.˜v
En ´eliminant ˜ I, on a: ˜v.(j.ω +h
m+k m.j.ω ) = −`.B m.˜u+`.B.˜v
R+j.L.ω
⇒˜v. h(j.ω +h
m+k m.j.ω ).R +`2.B2 mi=−`.B m.˜u
⇒˜v=−`.B
m.Um.ej.ω.t
(j.ω+h
m+k m.j.ω ).R+`2.B2 m
b. hv2i=
1
2.(`.B m.Um)2
(h
m.R+`2.B2 m)2+(R.ω−R.k m.ω )2=
1
2.(`.B.Um)2
[(h.R+`2.B2)2+(R.m.ω−R.k
ω)2]
2 Code avec Python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import scipy.optimize
3