enchainement d`operations

NOMBRES EN ECRITURE FRACTIONNAIRE (1)
I) Quotient de deux nombres
1) Définition
Le quotient d’un nombre a par un nombre b différent de 0 est égal à
a
b
.

Si a et b sont des nombres entiers,
0b
, le nombre
a
b
est appelé une fraction.
Exemples :
30 30:5 6
5
30
5
est un nombre entier
30
5
est une fraction
9,6 9,6:5,4 2,4
4
9,6
4
est un nombre décimal non
entier
9,6
4
n’est pas une fraction. Il
s’agit d’un nombre en écriture
fractionnaire
La division de 12,9 par 11 ne
« s’arrête » jamais.
12,9
11
n’est
pas un nombre décimal.
Cas particuliers
3,7 1
3,7 
0,83 0,83
1
00
98 
Exercices 1, 3, 4 p 31
Exercices 11, 12 page 32
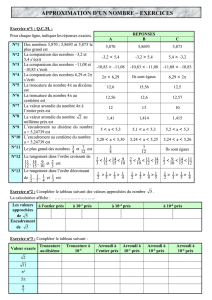
2) Troncature et arrondi
Pour obtenir la troncature au centième (par exemple) d’un quotient, il faut effectuer la division jusqu’à obtenir
un quotient avec deux chiffres après la virgule.
Exemples :
Troncature au centième de
5
6
: 0.83
Troncature au dixième de
8
9
: 0.8
Pour déterminer, par exemple, l’arrondi au dixième d’un nombre, on regarde le chiffre des centièmes de ce
nombre,
1) Si ce chiffre est 0, 1 ; 2 ; 3 ou 4, on garde le chiffre des dixièmes.
2) Si ce chiffre est 5, 6, 7, 8, ou 9, on ajoute un dixième.
dividende
diviseur
dénominateur
numérateur
a
ab b

Exemples :
Arrondi au dixième de 0,83 :
Arrondi au dixième de 0,68 :
Arrondi au centième de 0,837 :
Arrondi au centième de 0,684 :
Exercice 7 p 31
II) Quotients égaux
Voir activité 1 page 24 : « Quotients égaux »
1) Propriété
Un quotient ne change pas lorsqu’on multiplie ou lorsqu’on divise le numérateur (ou le dividende) et le
dénominateur (ou le diviseur) par un même nombre non nul.
a, b, c étant trois nombres quelconques :
b 0, 0
a a c a a c c
b b c b b c
Exemples :
21 21:3 7
15 15:3 5
5,8 5,8 10 58
3,1 3,1 10 31
4 7 4
7 3 3
Exercices 13, 14, 16 p 32
2) Simplification
Simplifier une fraction signifie trouver une fraction égale dont le numérateur et le dénominateur sont plus
petits.
Lorsqu’une fraction ne peut plus être simplifiée, on dit qu’elle est irréductible.
Exemples :
54 54:9 6
63 63:9 7
. On dit que la fraction
54
63
a été simplifiée par 9.
La fraction
6
7
ne peut pas être simplifiée.
6
7
est donc la fraction irréductible égale à la fraction
54
63
.
216 216:2 108 108:3 36
30 30:2 15 15:3 5
108
15
n’est pas une fraction irréductible. On peut la simplifier par 3.
36
5
est la fraction irréductible égale à la fraction
216
30
.
Exercices 20, 21 A B, 22 a ,b, c, d 25, 26, 30 p 33

III) Comment diviser un nombre par un nombre décimal ?
Voir activité 2 page 24-25 : « Division d’un nombre décimal par un nombre décimal »
Pour diviser à la main par un nombre décimal, on commence par multiplier le diviseur et le dividende par un
nombre (en général : 10, 100 ou 1000) de façon à rendre le diviseur entier.
Exemple :
Diviser 3,48 par 2,4 revient à diviser 34,8 par 24. En effet :
3,48 3,48 10 34,8
2,4 2,4 10 24
Exercices 31, 32, 33, 38, 41 p 34
IV) Comment multiplier des nombres en écriture fractionnaire ?
voir activité 3 page 43 : « Multiplication de deux nombres en écriture fractionnaire »
1) Savoir faire
Pour multiplier deux nombres relatifs en écriture fractionnaire :
1) on multiplie les deux numérateurs entre eux
2) on multiplie les deux dénominateurs entre eux
Notation : Soient a, b, c, d quatre nombres relatifs avec b et d non nuls (différents de 0), alors on a :
db ca d
c
b
a
En particulier :
11
c a c a c a c ac
ad d d d d
Ce qui revient à ne multiplier entre eux QUE les numérateurs
Exemples :
1 2 1 2 2
3 5 3 5 15
7 3 7 3 21
8 2 8 2 16
14 8 14 8 112
5 3 5 3 15
Cas particulier
2 3,5 2 3,5 2
3,5 9 1 9 1 9
Exercices 28 a b, 29 a b, 31 a b, 32 p 50 : Exercices 35, 38, 39 p 51
DM
Exercice 8 page 31
Exercices 21 C D page33, 22 e f g h page 33, 27 page 33
DM
Exercice 40 page 34
Exercices 28 c d , 29 c d, 31 c d page 50
Exercices 40, 41 page 51