Exercice III. Les lois de Newton (5,5 points)

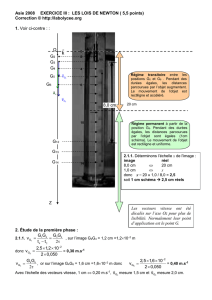
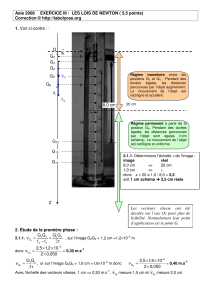
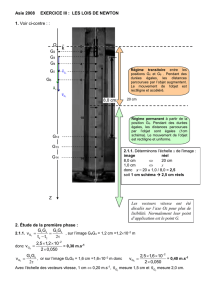
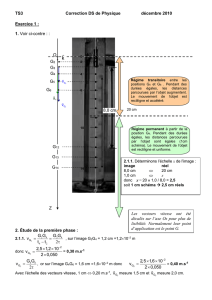
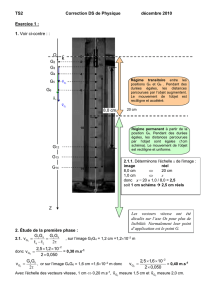
2.1.1. Échelle de l’image :
image réel
9,1 cm  20 cm
1,0 cm  2,2 cm
TS2 Correction du DM chutes verticales.
Exercice n°1
1.
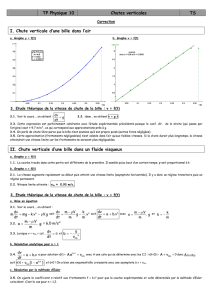
2. Étude de la première phase :
2.1.1.
3
2 4 2 4
42 2
GG G G G
vtt
,
3
2
G2,2 1,4 10
v2 0,050
= 0,31 m.s-1
5
46
2
GGG
v
,
5
2
G2,2 1,8 10
v2 0,050
= 0,40 m.s-1
Avec l’échelle 1 cm  0,20 m.s-1,
3
G
v
mesure 1,6 cm et
5
G
v
mesure 2,0 cm.
2.1.2.
5 3 5 3
44
22
G G G G
v v v v
v
aa
t
→
40,40 0,31
a2 0,050
= 0,90 m.s-2.
Avec l’échelle 1 cm  0,50 m.s-2,
4
a
mesure 1,8 cm.
2.2. Étude théorique
2.2.1. Poussée d’Archimède : = m’g = .V.g → = 1240  2,10.10-6  9,8 = 2,6  10–2 N
Poids de la bille :P = m . g →P = 3,80×10-3×9,8 = 3,7×10-2 N
37 14
26
P, ,
,
= 1,46 donc P et sont du même ordre de grandeur.
0
2
4
6
10
14
Z
O
Régime transitoire entre les
positions G0 et G8 .Le mouvement
de l’objet est rectiligne et accéléré.
Régime permanent à partir de la
position G9. Le mouvement de
l’objet est rectiligne et uniforme.
3
G
v
5
G
v
k
4
a

P
G
f
z
O
k
2.2.2. Référentiel terrestre supposé galiléen
Système : le solide
Inventaire des forces extérieures :
Auteur
Force
Vecteur
Terre
Répartie à
distance
Équivalente à
P mg
Fluide
Forces
pressantes
Réparties de
contact
Équivalente à
  Vg
Frottement fluide
Réparties de
contact
Équivalente à
f kv
2.3. Deuxième loi de Newton : Dans un référentiel galiléen, la somme des forces extérieures
appliquées à un système mécanique est égale au produit de la masse du système par le vecteur
accélération de son centre d’inertie G :
ext G
F m.a
.
2.4. En appliquant la deuxième loi de Newton au solide dans le référentiel du laboratoire galiléen :
P
+ +
f
=
G
m.a
 P.
k
– .
k
– f.
k
= m.az.
k
Au point G4 : P – – f4 = m.a4
f = P – – m.a4 = m.g – .V.g – m.a4
application numérique :
f = (3,7-2,6)10–2 – 3,8010–30,90 = 7,6 10–3 N.
2.5. L’énoncé donne : v4 = 0,32 m.s-1Or : f = k.v4 → k =
4
f
v
→ k =
3 8,0 10
0,32
= 2,410–2 kg.s-1
( car f en N avec N = kg.m.s-2 et v en m.s-1).
3. Étude de la deuxième phase
3.1. Durant la seconde phase, en régime permanent, le mouvement est rectiligne et uniforme.
3.2. Première loi de Newton (principe d’inertie) : Dans un référentiel galiléen, si la somme vectorielle des
forces extérieures appliquées à un solide est nulle alors ce dernier est soit immobile, soit son centre
d’inertie a un mouvement rectiligne et uniforme.
3.3. On a :
P
+ +
f
=
0
 P – – flim = 0  P – – k.vlim = 0
 vlim =
Pk
 vlim =
–2
-1
–2
3,7-2,6 ×10 = 0,44 m.s
2,4×10
3.4.
13
12 14
2
GGG
v
→
5
2
G2,2 2,3.10
v2 0,050
= 0,51 m.s-1
Soit 11% d’écart avec la vitesse limite calculée.

Exercice n°2
1. Mesure de la viscosité  de la glycérine
1.1.
1.2. Poids de la bille : P = mbille.g. or  =
mV
bille
donc P = .V.g
1.3. Poussée d’Archimède :
A
P
= m0.g. où m0 est la masse de glycérol déplacé par
la bille, donc PA = 0.V.g.
1.4.1. La vitesse limite est atteinte avant le passage au niveau de R1. Entre les
deux repères R1 et R2, le vecteur vitesse
v
de la bille est un vecteur
constant : la bille a un mouvement rectiligne et uniforme.
1.4.2. D’après la deuxième loi de Newton :
ext G
F ma
Or
0
G
GG
dv
a car v est un vecteur constant
dt
donc
P
+
A
P
+
f
=
0
.
1.5.1. On a : f = 6 . .r.v
Analyse dimensionnelle : [] =
211
1
f m . a M.L.T M.L .T
r . v r . v L.L.T
Donc  s’exprime en kg.m-1.s-1.
1.5.2.
P
+
A
P
+
f
=
0
 .V.g
j
– 0.V.g
j
– 6..r.vlim
j
=
0
 .V.g – 0.V.g – 6..r.vlim = 0
 V.g.( – 0) = 6..r.vlim   =
0
6lim
V.g .
.r.v   
Or :
3
4
3
Vr
donc en reportant :  =
30
4
36lim
g
r . .
.r.v
20
2
9lim
r .g.v
1.6.1. vlim=
ht'
→ vlim =
2
40 0 10
1 66
,,
= 0,241 m.s-1.
1.6.2.
20
2
9lim
r .g.v
 =
2
3 3 3
2 5 00 10 9 81 7 80 10 1 26 10
9 0 241
, , , ,
,
= 1,48 kg.m-1.s-1
1.6.3. thé= 1,49 SI. écart relatif :
100 thé
thé
1 49 1 48
100 1 49
,,
,
0,7 %.
2. Étude théorique du mouvement de la bille
2.1. On applique la deuxième loi de Newton à la bille, de masse m, dans le référentiel terrestre supposé
galiléen :
ext
F m.a
P
+
A
P
+
f
=
m.a
.V.g.
j
– 0.V.g.
j
– 6..r.v
j
= .V.
dv
dt
 .V.g – 0.V.g – 6..r.v = V.
dv
dt
dv
dt
= g –
0
.g –
6. .r.v
.V
=
06
1r g. .v
V
dv
dt
+
6r.v
V
=
0
1g.
en identifiant avec l’équation:
dv
dt
+ A.v = B A =
6. .r
.V
et B =
0
1g.
j
O
y
P
A
P
f

2.2. Vitesse limite atteinte par la bille : v = vlim = cte alors
dv
dt
= 0 donc A.vlim = B soit vlim =
B
A
vlim =
8 23
34 4
,,
= 0,239 m.s-1 or en 1.6.1. on a mesuré vlim,exp = 0,241 m.s-1
La valeur vlim est en accord la valeur expérimentale vlim,exp : écart relatif de 0,8 %.
2.3. Le rapport
Error!
s’exprime en s (car A s’exprime en s-1). Donc A est homogène à une durée : A
correspond à la durée caractéristique de chute de la bille dans la glycérine.
Considérons l’équation différentielle à la date t = 0 s :
0t
dv
dt 
+ A.v(t=0) = B
La bille est lâchée sans vitesse initiale v(t=0) = 0 donc
0t
dv
dt 
= B
Donc B correspond à l’accélération de la bille à la date t = 0 s.
2.4.1. Le pas t est : t = ti+1 – ti = 0,025 – 0,020 = 0,005 s = 5 ms.
2.4.2. méthode d'Euler : v6 = v5 + a5.t
v6 = 0,146 + 3,20  510–3 = 0,162 m.s-1
a7 = (B – A.v7)
a7 = 8,23 – 34,4  0,175 = 2,21 m.s-2
2.5.1. & 2.5.2.