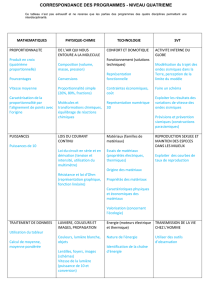
Rappels calculs numériques

M. DESERT EG4 MATHEMATIQUES SECONDE PRO 1
RAPPELS :
 FRACTIONS IRREDUCTILES
 POURCENTAGES
 PROPORTIONNALITE
 PUISSANCE D’UN NOMBRE
 PUISSANCES DE 10 ET NOTATION
SCIENTIFIQUE
 RACINES CARRES
 DEVELOPPEMENT D’UNE EXPRESSION
 FACTORISATION D’UNE EXPRESSION

M. DESERT EG4 MATHEMATIQUES SECONDE PRO 2
Fractions irréductibles
Objectif
Le PGCD de 2 nombres entiers permet de mettre les fractions sous forme irréductible.
Comment simplifier des fractions grâce aux critères de divisibilité ou au PGCD ?
1. Simplifications de fractions
On dit que l’on simplifie une fraction lorsqu’on l’écrit avec un numérateur et un
dénominateur plus petits.
En pratique, cela revient à diviser le numérateur et le dénominateur par un même nombre.
Exemple : simplifier
15 et 75 sont divisibles par 5 car leurs chiffres des unités est 5. On a donc :
Remarque : On peut présenter la simplification d’une fraction en barrant les facteurs
communs du numérateur et du dénominateur.
2. Fractions irréductibles
Une fraction est irréductible lorsque l’on ne peut plus la simplifier.
Exemple :
Remarque : on peut donc rendre une fraction irréductible en connaissant les critères de
divisibilité.
Définition équivalente : Une fraction est irréductible si le PGCD (a ; b) = 1
Autrement dit : Une fraction est irréductible si a et b sont premiers entre eux.
Exemple : est une fraction irréductible car PGCD (43 ; 65) = 1

M. DESERT EG4 MATHEMATIQUES SECONDE PRO 3
Propriété : Si on divise le numérateur et le dénominateur d’une fraction par le PGCD (a ;
b), alors la fraction obtenue est irréductible.
Application : Rendre la fraction irréductible
1ère étape : Calcul du PGCD par algorithme d’Euclide
• On effectue la division euclidienne de 10608 par 391.
On obtient : 10608 = 27 × 391 + 51
• Puis : 391 = 7 × 51 + 34
• Puis 51 = 1 × 34 + 17
• Puis 34 = 2 × 17 + 0
Donc PGCD (10608 ; 391) = 17 (car 17 est le dernier reste non nul)
2ème étape : simplification de fractions :
est une fraction irréductible.

M. DESERT EG4 MATHEMATIQUES SECONDE PRO 4
Pourcentages
1. Des clés pour ne plus se tromper

M. DESERT EG4 MATHEMATIQUES SECONDE PRO 5
2. Part en pourcentage