le monopole

LE MONOPOLE
Dans un monopole, contrairement à une situation de concurrence pure et parfaite, il n'y a
qu'un seul producteur pour un bien. Il entraîne la présence de plusieurs facteurs :
- Existence de brevets, droits d'auteur.
- Contrôle des ressources spécifiques
- Structure de coûts décroissants (on parle de monopole naturel).
- Existence de cartels (Exemple : L'OPEP)
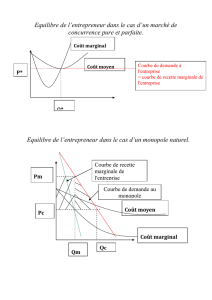
 Forme de la courbe de demande dans un monopole.
- On observe une pente négative, qui se traduit par une relation négative entre la
quantité et le prix du bien.
A
1 2
p
Si
1p
, alors nous avons
5q
.
Si
2p
, alors nous avons
4q
.
Si
3p
, alors nous avons
3q
.
 Le choix du niveau de production du monopoleur est défini en fonction du maximum
de son profit.
 Or nous savons que la Recette Totale est :
RT p q q
, et, par conséquent,
RM p q
( ce qui correspond à la courbe de demande), mais également,
p q q
RT q p q
Rm p q q
q q q
.
 Exemple d'une fonction de demande linéaire :
p q a q b  
(avec
0a
et
0b
) :
On a :
2
RT p q q a q b q     
, d'où
RM a q b  
et
2Rm a q b  
.
On peut remarquer que la pente de la recette marginale est deux fois élevée que la pente de la
recette moyenne, c'est-à-dire de la courbe de demande.
Les implications d'une demande linéaire sont :
- La courbe de recette marginale n'est plus confondue avec celle de la recette moyenne.
- La recette moyenne est décroissante, donc on se situe en dessous de celle-ci.
- Recette moyenne et recette marginale sont des droites et la pente de la recette
marginale est deux fois plus élevée que celle de la recette moyenne.

- Au point
*q
, la recette totale est maximale, c'est-à-dire que la recette marginale est
nulle
0Rm 
.
- A gauche de
*q
, la recette totale augmente avec
q
, alors nous avons
0Rm 
.
On sait que
2
RT a q b q q a q b      
, donc
0RT 
si et seulement si
0q
ou
p
qa
.
RT
*q
b
Rm
RM
*q
RM a q b  
d'où
RM b
si et seulement si
0q
et
0RM 
si et seulement si
b
qa
 Recette et élasticité-prix de la demande :
L'élasticité de la demande permet de mesurer la sensibilité des variations relatives de la
quantité demandée suite aux variations de prix relatives, on a la relation suivante :
0
pqp
pq
.
Or, nous savons que :
RT q p q p
Rm q p q q p q p
q q p q
,
D'où :
11
11
pp
Rm q p q p q
.
 Profit de monopole :
q RT q CT q p q q CT q
.
D'après la condition de premier ordre ( CPO ), on a :
0
q
q
, d'où
Rm q Cm q
,

Ou encore :
1
1
p
Cm p q
.
A l'optimum, nous avons
0Cm 
, et donc, par conséquent,
0Rm 
, et
1
p
.
C'est pour cela que le monopoleur va produire dans la 3éme partie élastique de la courbe de
demande.
1
p
1
p
1
p
RM
0
q
q
Rm
 Résumons ceci sous forme d'un tableau :
p
Rm
p
1
: Elastique
0
Rm
1
: Unitaire
0
Rm
1
: Inélastique
0
Rm
La condition d'optimalité nous dit :
1
1
p
Cm q p q
, d'où
11
1
p
p q Cm q
.
Or, on sait que
1
p
, on a alors :
1 1 1
1 1 1 1
1
1
pp
p
, ce qui nous amène à :
p q Cm q
.

 A l'optimum du monopole :
Cm
*p
Cm
RM
*q
Rm
On a, à l'optimum, la relation
Rm Cm
avec
1
1
p
Cm p q
. Dans un monopole, le
prix est majoré par un facteur égal à
1
1
p
.
 Le monopole naturel : (Exemple de coûts décroissants)
p
CM
Cm
q
*q
On sait que
q q p Cm
, d'où
p Cm
lorsque
0
q
q
.
 Comportement du monopole : Stratégie de prix plus complexe.
 Démonstration par les prix : Capacité d'une entreprise à vendre un même bien à des
prix différents en fonction des acheteurs ou des segments de marchés.
 Il existe 3 formes de discriminations :
- Discrimination au premier degré : C'est le fait de faire payer le prix maximum
par consommateur en fonction de sa volonté de payer.
- Discrimination du second degré : Le prix par unités d'output dépend de la
quantité consommée ( différences entre gros et petit consommateurs ).

- Discrimination du troisième degré : Le prix diffère en fonction des individus
(groupes) mais le prix est le même pour tous les individus d'un même groupe.
Dans ce cas, nous avons deux courbes de demandes
11
pq
et
22
pq
, nous
sommes en mesure d'identifier les deux groupes, le même produit est vendu
aux deux groupes, il n'y a pas de possibilités de revendre le produit et le coût
de production est
12
c q q
.
 Problème de maximisation :
1 1 1 2 2 1 2
Max q p q q p q c q q
D'après la condition de premier ordre :
1 1 1 2
1
0
qRm q Cm q q
q
2 2 1 2
2
0
qRm q Cm q q
q
.
 Implication :
Le coût marginal est le même sur les deux marchés. A l'optimum, on a donc
1 1 2 2
Rm q Rm q
.
On sait que
1
1
p
Cm q p q
, d'où
1 2 1 1
1
1Cm q q p q
et
1 2 2 2
1
1Cm q q p q
.
Cm
est donc le même pour les deux groupes :
12
12
11
11p q p q
Si
1 1 2 2
p q p q
, alors
12
11
11
et donc on a :
12
 Conclusion :
Les prix payé par un groupe de consommateurs va dépendre de l'élasticité prix de ce groupe.
Ainsi, le marché avec les prix le plus élevé est celui avec l'élasticité la plus faible.
 Monopole avec 2 marchés :
Nous prenons comme hypothèses que
0Cm 
.
Nous avons les fonctions de demandes suivantes :
11
q b a p  
et
22
q b a p  
, d'où les
fonctions de demandes inverses :
1
1bq
pa
et
2
2bq
pa
.
Ainsi, les fonctions de recette totale sont :
2
1 1 1 1 1
1b
RT p q q q
aa
et
2
2 2 2 2 2
1d
RT p q q q
cc
, d'où
11
2b
Rm q
aa
et
22
2d
Rm q
cc