Théorème de Thalès

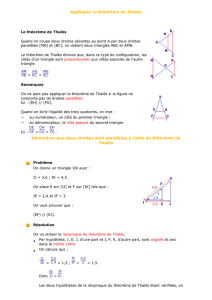
Théorème de Thalès.
Applications à la géométrie du plan et de l’espace
Le théorème de Thalès fait partie des théorèmes que l’on rencontre pour la première
fois au Collège. Tout d’abord sous la forme du théorème des milieux, puis dans la
configuration d'un triangle coupé par une droite parallèle à l'un des côtés.
Pré requis :
- Aire d’un triangle.
- Droite orientée.
- Mesure algébrique.
- Application affine et application linéaire associée.
- Calcul vectoriel.
Cadre :
ur
On se placera dans le plan P et l’espace E en tant qu’espaces affines euclidiens, en notant P
ur
et E leurs espaces vectoriels associés.
Plan :
IIIIIIIVV-
Configuration triangulaire de Thalès.
Théorème de Thalès dans le plan.
Théorème de Thalès dans l’espace.
Projections dans le plan et l’espace.
Théorème de Ménélaüs.
Démonstrations proposées :
- Théorème de Thalès dans le plan.
- Théorème de Ménélaüs.
Rappel :
Axiome de Pasch :
Étant donné trois points A, B, C, non alignés, si une droite D ne passant par aucun des
sommets du triangle ABC, rencontre l'un des segments ]AB[, ]BC[, ]CA[, alors elle en
rencontre un autre.
I-
Configuration Triangulaire de Thalès.
Théorème 1 :
Soient ∆1 et ∆2 deux droites strictement parallèles du plan P, et soient D et D’ deux
droites sécantes en O, non parallèles à ∆ 1 , qui coupent respectivement les droites ∆1 et ∆2 en
OB OB '
A, B et A’, B’. On a alors
=
; O,A,B et O, A', B' sont dans le même ordre.
OA OA '
Preuve :
1) On veut montrer que O, A, B sur D et O, A’, B’ sur D' sont dans le même ordre. Pour cela
supposons que le point A appartienne à ]OB[.
Alors, ∆ 1 coupe ]OB[, comme ∆ 1 ne passe pas par O – elle serait alors confondue avec D – et
ne passe pas par B' – elle couperait ∆ 2 – l’axiome de Pasch assure alors qu’elle coupe ]BB’[
ou ]B’O[.
Supposons qu’elle coupe ]BB’[ en M.
Alors ∆1 ne serait pas strictement parallèle à ∆2, donc ∆1 coupe]OB’[.
Si c'est le point B qui appartient à ]OA[, une démonstration analogue à la précédente point
par point, montre que B' appartient à ]OA'[.
OB OB '
=
.
OA OA '
En notant hB la hauteur issue de B et hB’ la hauteur issue de B’, on a :
1
1
A (OBB ') OB
A (OBB′) = OB.h B ′ et A (OAB′) = OA.h B ’ . D′où
=
.
2
2
A (OAB ') OA
A (OBB ') OB '
De même, A (OBB′) =OB′.h B et A (OA′B) =OA’.h B . D’où
=
.
A (OA ' B ) OA '
Montrons alors que A (OAB′)= A (OA′B).
A (OBB′)= A (OAB′) + A (ABB′), car A est entre O et B, et donc ABB’ et OAB’ ont une
intersection réduite au segment [AB’]. De même, A’ étant entre O et B’, on a
A (OBB′)= A (OBA′) + A (A’BB′). On en déduit que A (OAB′)= A (OA′B).
OB OB '
Et donc
=
.
OA OA '
2) On veut monter alors que
Remarque : Le théorème que nous venons d’énoncer est un cas particulier du théorème de
Thalès. Un cas plus général est énoncé ci-après.
II- Théorème de Thalès dans le plan.
Théorème 2 :
Soient D1, D2, et D3 trois droites strictement parallèles, et soient d et d’ deux droites
non parallèles à D1 qui coupent respectivement D1, D2, et D3 en A, B, C et en A’, B’, C’.
On a alors :
A ' C ' AC
=
.
A ' B ' AB
Démonstration :
• Si d est parallèle à d’, le résultat est immédiat puisqu’on obtient deux
parallélogrammes.
• On suppose alors d et d’ sécantes. On note O leur point d’intersection.
On considère l’homothétie h de centre O qui transforme A en B et h’ l’homothétie de centre
O qui transforme A en C.
uuur
uuur
uuur
uuur
Alors il existe α et β appartenant à Ë, tels que : OB = α OA et OC = β OA .
uuur uuur uuur
uuur
uuur
uuur
On a alors : AC = AO + OC = ( β − 1 ) OA et AB = ( α − 1 ) OA .
uuur uuur
Si α = 1, OB = OA et donc D1 = D2 ce qui est impossible.
uuur
uuur β − 1 uuur
1 uuur
On peut alors écrire: OA =
AB d’où AC =
AB .
α −1
α −1
De plus h(A)=B et h′(A′)=K où K est l’intersection de (OA’) et de la parallèle à (AA’)
passant par B.
uuuuur β − 1 uuuuur
Donc h(A′)=B′. On a alors A ' C ' =
A' B ' .
α −1
Par le même raisonnement, h′(A′)=C ′.
De plus A, B et C sont alignés, ainsi que A’,B’ et C’.
A ' C ' AC
En passant aux mesures algébriques, on a :
=
.
A ' B ' AB
Proposition 3: (Réciproque du théorème de Thalès).
Soient deux droites d et d’ et trois droites D1, D2 et D3 coupant respectivement d et d’
en A, B, C,distincts deux à deux, et A’, B’, C’,distincts deux à deux.
A ' C ' AC
=
, alors D3 est parallèle à D1 et D2.
Si D1 est parallèle à D2 et si
A ' B ' AB
Démonstration :
Soit D '3 la parallèle à D1, passant par C qui coupe d’ en K.
A ' B ' AB
A ' C ' AC
=
= et comme par hypothèse,
=
, alors
A' K
AC
A ' B ' AB
A ' K = A ' C ' , et comme A’, K et C’ sont alignés, on a K = C', d’où D3 = D '3 , et D 3 est
parallèle à D1, et à D2..
D’après le théorème direct,
III-
Théorème de Thalès dans l’espace.
Théorème 4 :
Soient P1 , P2 et P3 trois plans strictement parallèles, et D et D’ deux droites non
parallèles à P1 .
On note A, B, C, les points d’intersection de D avec P1 , P2 et P3 . On note également A’, B’,
C’ ceux de D’ avec P1 , P2 et P3 . Alors :
A ' C ' AC
=
.
A ' B ' AB
Démonstration :
Si D et D’ sont coplanaires, on est ramené au cas du théorème de Thalès dans le plan.
On suppose donc D et D’ non coplanaires. On trace la parallèle D1 à D’ passant par A.
Elle coupe P2 en B1 et P3 en C1 . On est alors ramené au cas plan du théorème de Thalès dans
le plan déterminé par D et D1.
AC AC1
Ainsi,
=
.
AB AB1
Dans le plan déterminé par D1 et D’, on obtient
Donc
AC1 A ' C '
=
.
AB1 A ' B '
A ' C ' AC
=
.
A ' B ' AB
Proposition 5 :
Si trois points A, B et C, d’une droite D et trois points A’, B’ et C’, d’une droite D’
A ' C ' AC
=
, et si D et D’ ne sont pas coplanaires, alors il existe un plan de l’espace
vérifient
A ' B ' AB
auquel les trois droites (AA’), (BB’) et (CC’) sont parallèles.
Démonstration :
Soit deux droites D et D’ non coplanaires.
On a alors (AA’) non parallèle à (BB’), car sinon le plan défini par les droites (AA’) et (BB’)
contiendrait D et D’.
Soit (Ax) la parallèle à (BB’) passant par A, et (By) la parallèle à (AA’) passant par B.
Le plan P1 défini par (AA’) et (Ax), et le plan P2 , défini par (BB’) et (By), sont parallèles car
deux sécantes de l’un sont parallèles à deux sécantes de l’autre.
Soit P le plan passant par C parallèle à P1 et P2 .
Il coupe D’ en K et d’après le théorème de Thalès dans l’espace :
A ' B ' AB
=
.
A' K
AC
A ' C ' AC
=
, donc A ' K = A ' C ' , et comme A’,C’ et K sont alignés, K = C’.
A ' B ' AB
Les trois droites sont donc bien dans trois plans parallèles.
Or
Remarque :
Cet énoncé ne constitue pas une réciproque du théorème de Thalès dans l’espace.
IV-
Projections dans le plan et l’espace.
I)
Dans le plan.
Rappel :
Dans le plan, étant donné un point M et une droite D’, il existe une seule droite d M
passant par M et parallèle à D’. Si D est une droite non parallèle à D’, d M et D sont alors
sécantes en un point m.
Définition 6 :
L’intersection de D avec la droite passant par M et parallèle à D’ est appelée le projeté
de M sur D parallèlement à D’. L’application qui à tout point M du plan associe son projeté m
sur D parallèlement à D’, s’appelle la projection ponctuelle sur D parallèlement à D’.
Proposition 7 : (Traduction du théorème de Thalès en terme de projection)
Soient D et D’ deux droites non parallèles, etuuur
A, B etuuu
C,
r trois points du plan.
= λ AB , alors les projetés A’, B’, C’ de
Si A, B, C sont alignés, il existe un réel λ tel que ACuuuuur
uuuuur
A, B, C sur D parallèlement à D’ vérifient également A ' C ' = λ A ' B ' .
Démonstration :
(Utilisation direct du théorème de Thalès).
Proposition 8 :
Les projections conservent les milieux.
Démonstration :
Cas particulier de la proposition 7. Il suffit de prendre λ = 2.
Proposition 9 :
L’image d’un parallélogramme par une projection ponctuelle est un parallélogramme
aplati. (On parle de conservation de l’équipollence).
Démonstration :
Soit ABCD un parallélogramme.
uuur uuur
Alors AB = DC , et [AC] et [BD] ont même milieu. D’après la proposition 8, [A’C’] et
[B’D’] ont même milieu. Donc A’B’C’D’ est un parallélogramme. De plus A’, B’, C’ et D’
sont alignés, donc A’B’C’D’ est un parallélogramme aplati.
Dans l’espace.
II)
Rappel :
Dans l’espace, étant donné un point M et un plan P, il existe un seul plan PM passant
par M et parallèle à P. Si D est une droite non parallèle à P, PM et D sont sécants en un point
m.
Définition 10 :
L’intersection de D avec le plan passant par M et parallèle à P, est appelée le projeté de
M sur D parallèlement à P. L’application qui à tout point M de l’espace, associe son projeté m
sur D parallèlement à P, s’appelle la projection ponctuelle sur D parallèlement à P.
Définition 11 :
L’intersection de P avec la droite passant par M et parallèle à D, est appelée projeté de
M sur P parallèlement à D. L’application qui à tout point M de l’espace associe son projeté m
sur P parallèlement à D, s’appelle la projection ponctuelle sur P parallèlement à D.
III)
Projection vectorielle associée dans le plan.
Définition 12 :
ur
Dans le plan, soit p la rprojection sur D parallèlement à D’. L’application
de
P dans
uur
uuur
lui-même
qui à tout vecteur u de représentant AB associe le vecteur u ' de représentant
uuuuur
A ' B ' avec A’ et B’ les projetés de A et B par p, est appelée projection vectorielle associée à
la projection ponctuelle p. On la note Π.
Proposition 13 :
r r Π est
ur une
ur application linéaire:
∀ u , v ∈ P × P , ∀ α ∈ R , on a :
r r
• Π u+ v = Π
r
• Π α u = αΠ
(
)
(
(
)
)
r
r
( ru ) + Π ( v )
( u) .
;
Démonstration
r : ur
r uuur
• Soit ru ∈ P avec u = AB . uuur
uuur
∀ α ∈ R , α u a pour représentant AC = α AB .
Alors, d’après le théorème de Thalès :
uuuuur uuuuur
α A ' B ' = A ' C ' , c'est-à-dire :
Si A’, B’, C’ sont les projetés
de
A,
B
et
C
par
p,
on
a
uuur
r
r
uuur
uuur
α.Π( AB ) = Π( AC ) = Π(α. AB ) et donc Π(α. u ) = α.Π( u ).
•
uuur r
uuur r
r r
ur ur
Soit ∀ u , v ∈ P × P , et A, B, C trois points de P avec AB = u et BC = v .
(
)
Si A’, B’, C’
les projetés
B et C par p, on a :
r sontuuuuu
r de A,
uuuuur
r
'C ' .
Π( u r) = A ' Br' et Π( v ) = Buuuuur
uuuuur
uuur
r r
uuuuur
uuur uuur
Et donc, Π( u ) + Π( v ) = A ' B ' + B ' C ' = A ' C ' = Π( AC ) = Π( AB + BC ) = Π( u + v ).
Remarque :
Par ce procédé, on vient de démontrer que Π est une application linéaire et donc que p
est une application affine.
IV)
Projection vectorielle associée dans l’espace.
Dans l’espace, on définit de la même manière la projection vectorielle associée à la projection
ponctuelle sur P parallèlement à D ou la projection vectorielle sur D parallèlement à P. Sa
linéarité entraîne le caractère affine de p.
V- Théorème de Ménélaüs dans le plan
Théorème 14 :
Soit un triangle ABC, et trois points tels que A’ soit sur (BC), B’ soit sur (AC), C’ soit
sur (AB), tous trois distincts des sommets.
A' B B 'C C ' A
×
×
= 1.
Si A’, B’ et C’ sont alignés, alors on a l’égalité suivante :
A'C B ' A C ' B
Démonstration :
Supposons A’, B’, C’, alignés sur une droite ∆.
Soit p la projection sur (AC) parallèlement à ∆. Les points A, B, C’, C, A’ ont respectivement
pour images A, B1, B’, C, B’.
D’après le théorème de Thalès :
C ' A B' A
C ' A B ' B1
A ' B B ' B1
A' B B ' C
=
⇔
×
= 1 , et
=
⇔
×
= 1.
C ' B B ' B1
C 'B B' A
A'C B 'C
A ' C B ' B1
D’où le résultat, en multipliant entre elles les deux égalités à 1.
Remarque :
Le théorème que l’on vient d’énoncer admet une réciproque qui n’utilise pas
directement le théorème de Thalès. C’est pourquoi elle n’est pas mentionnée. Le Théorème de
Ménélaüs admet également un énoncé dans l’espace.