v4 - Bissectrices, distances et tangente

v4 - Bissectrices, distances et tangente 19/01/2015 16:21:0006/04/2015 21:51:00
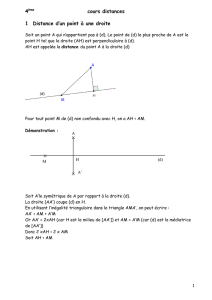
Distance et tangente
Définitions
La distance entre deux objets est la longueur du plus court
chemin reliant ces deux objets.
Si un objet est à la même distance de deux autres, ont dit qu’il
est équidistant des deux autres.
M
A
B
M est équidistant de A et B
Propriétés admises
1 Si un point est équidistant des extrémités d’un segment, alors
il est sur la médiatrice de ce segment.
2 Si un point est sur la médiatrice d’un segment, alors il est
équidistant des extrémités du segment.
A x
x B

v4 - Bissectrices, distances et tangente 19/01/2015 16:21:0006/04/2015 21:51:00
Propriété admise
L’ensemble des points équidistants à deux points A et B est la
médiatrice du segment [AB].
A
B
Propriété admise
Le point équidistant à trois points A, B et C non alignés est le
centre du cercle circonscrit au triangle ABC.
Le centre du
cercle circonscrit
est le point
d’intersection des
médiatrices des
trois côtés du
triangle.
Il suffit d’en
tracer deux pour
obtenir le point
d’intersection, mais
le tracé des trois
permet de contrôler
son tracé.
A
B
C

v4 - Bissectrices, distances et tangente 19/01/2015 16:21:0006/04/2015 21:51:00
Définition
Soit (d) une droite et A un point n’appartenant pas à (d).
La distance entre la droite (d) et le point A est la longueur du
segment [AH] où H est le point de (d) tel que (AH) ⊥ (d).
H
(d)
A
Propriétés admises²
1 Si un point est équidistant des demi-droites formant un
angle, alors il est sur la bissectrice de cet angle.
2 Si un point est sur la bissectrice d’un angle, alors il est
équidistant des demi-droites formant cet angle.

v4 - Bissectrices, distances et tangente 19/01/2015 16:21:0006/04/2015 21:51:00
Propriété admise
Les bissectrices d'un triangle sont concourantes en un point
appelé le centre du cercle inscrit au triangle.
Comment tracer le cercle inscrit à un
triangle ?
1. Tracer les bissectrices des 3
angles de la figure ; on trouve le
centre du cercle inscrit. Tracer 2
bissectrices suffit, mais on ne peut
pas vérifier.
2. Tracer la perpendiculaire à un côté
qui passe par le centre du cercle
inscrit ; c’est la distance entre le
centre et le triangle.
3. Tracer le cercle dont le rayon est
cette distance et dont le centre est
le centre du cercle inscrit.
Définition
Soit C un cercle de centre O et A un point du cercle.
On dit que la droite (d) est la tangente au cercle C au point A
si :
A ∈ (d)
(OA) ⊥ (d)
O
A

v4 - Bissectrices, distances et tangente 19/01/2015 16:21:0006/04/2015 21:51:00
Propriété admise
Un cercle et une droite peuvent être :
disjoints tangents sécants
Ils n’ont aucun point
d’intersection. Ils ont un seul point d’intersection. Ils ont deux points d’intersections.
Propriété admise
Soit ABC un triangle.
Soit G le centre de gravité
du triangle et M le pied de la
médiane issue de A.
2
alors AG = AM
3
A
CB
M
G