les diagrammes binaire S-L

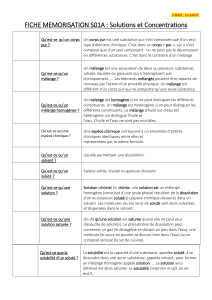
Chapitre : diagrammes binaires : solide -liquide
Introduction :
Les équilibres binaires liquide-solide vont être étudiés par analogie avec les équilibres binaires vapeur-
liquide. Par hypothèse, les constituants A1 et A2 seront toujours totalement miscibles à l’état liquide.
Par contre les solides pourront être :
 Soit totalement miscibles : analogie avec les solutions liquides idéales ou non ;
 Soit totalement non miscibles : analogies avec deux liquides non miscibles.
Rappelons que désormais la pression est quasi sans influence sur ces équilibres (phases condensées). On
travaille donc usuellement à P fixée, la pression atmosphérique, et on ne considère plus que les diagrammes
isobares.
Ces diagrammes sont très importants en métallurgie : étude des alliages notament…
I)Miscibilité totale à l’état solide :
L’analyse thermique permet d’établir les diagrammes isobares. Le fait de retrouver soit des fuseaux
simples soit des courbes avec extremum nous permet d’étendre la notion de solutions idéales aux solutions
solides.
1)solutions quasi-idéales :
a)diagramme isobare :
Le diagramme obtenu ne présente pas d’extremum (fig.1).
Figure : 1
Il s’agit de deux solides de propriétés physiques très voisines (citons le ces de l’argent et de l’or) :
 Cristallisation dans un même système (cfc),
 Arête de maille identique (408pm),
 Rayon métallique quasi identique (144pm),
Ce qui leur permet d’avoir des rôles interchangeables dans le réseau cristallin (miscibilité) et sans
interactions mutuelles nouvelles (idéalité) : solution solide dite de substitution.

Il existe également des solutions solides d’insertion, l’un des éléments occupant les sites du réseau
cristallin de l’autre. Mais dans ce second cas, la maille est déformée. L’analyse par diffraction des rayons X
ou par microphotographie (microscope électronique) permet de visualiser ces cristaux.
Pour chaque constituant d’une solution solide idéale, on peut poser :
s
i
S
Ti xRT ln
0)( 
s
i
Les températures d’ébullition sont désormais remplacées par les températures de fusion
*
1
T
et
*
2
T
.
Remarquons que le composé le plus fusibles a la température de fusion la plus basse. Les courbes de rosée
et d’ébullition sont remplacées par le solidus et le liquidus.
Le liquidus donne le début de cristallisation de tout mélange liquide : courbe
)( 2
l
xfT 
.
Le solidus donne le début de fusion de tout mélange solide : courbe
)( 2
S
xgT 
.
Remarque : on utilise également fréquemment les diagrammes
),( 22 Sl wwfT 
, le titre massique étant
souvent plus commode que le titre molaire pour les solides.
a)analyse thermique :
On peut suivre à l’aide d’un thermomètre suffisamment précis (ou d’un thermocouple), la variation de la
température en fonction du temps d’un mélange binaire initialement liquide. On obtient la courbe suivante
(fig.2).
Partons d’une solution de composition connue
21
2
2mm m
WM
. Le refroidissement isobare correspond à
la portion MN. En N apparait la première phase solide (ces cristaux ont leur composition donnée par N’) :
La phase solide est plus riche en 2 que la phase liquide, c’est-à-dire en composé le moins fusible
*
2
*
1TT 
.
Pendant le changement d’état (NP’), la température baisse plus lentement en raison de la lenteur des
équilibres et du fait que la solidification libère de l’énergie thermique.
La composition de la phase liquide décrit le chemin curviligne
PN 
et celle de la phase solide le chemin
'' PN 
. En P’, le mélange est entièrement solidifié, et la portion P’Q correspond à son refroidissement
isobare jusqu’à la température ambiante. En opérant pour diverses compositions connues initiales, on
détermine expérimentalement un ensemble de points N (liquidus) et de point P’ (solidus), et l’on peut
tracer le diagramme isobare.

c)Théorème de l’horizontale et le théorème des moments :
-Théorème de l’horizontale :
Tout mélange diphasé G a la composition de chacune de ses phases, solide ou liquide, donnée par le tracé
d’un segment horizontal et les intersections respectives avec solidus et liquidus.
-Théorème des moments :
En écrivant la conservation de la masse totale m0 et la conservation de la masse initiale de A2, nous
obtenons (fig.3).
GSmGLmSl 0
Avec dans chaque phase :
lll mwm 22 
et
SSS mwm 22 
Sous une forme plus pratique :
LS
GS
mml0
et
LS
LG
mmS0
2)solutions non idéales :
a) diagramme isobare :
Désormais les diagrammes peuvent présenter un extremum. Il s’agit en général d’un minimum de T sous P
fixée (Patm) : (fig.4)
Figure : 4
Figure : 3

Citons le cas du cuivre et de l’or : il s’agit toujours de deux solides de même réseau cristallin (ici cfc) pour
conserver la miscibilité mais des différences dans les paramètres géométriques (rCu=128pm et rAu=144pm)
provoquent des interactions mutuelles nouvelles. Dans une telle solution solide, le potentiel chimique se
met sous la forme :
s
i
S
Ti aRT ln
*)( 
s
i
avec
S
i
S
i
S
ixa
Nous retrouvons un comportement idéal à la limite :
1
lim
1 i xS
i
Nous constatons l’existence de l’analogue d’un azéotrope. Le point I pour lequel les deux phases ont la
même composition est appelé point indifférent.
Le refroidissement d’un liquide, de composition initiale celle du point indifférent I, aboutit à une
solidification à température et pression constantes (analogie avec le corps pur : palier de changement
d’état). Lorsque l’on modifie la pression (peu d’influence sur les phases condensées), la composition du
point indifférent varie très peu (différence avec l’azéotrope).
L’analyse en termes de variance du diagramme isobare précédent se fait comme précédemment :
 3V'
à P fixée.
 Domaine L (ou S) :V’=2 ; T et x2 libres ….
 Domaine L+S : V’=1 ;
)( 2
l
xfT 
et
)( 2
S
xgT 
 La nouveauté concerne le point I ou en plus
Sl xx 22 
. Alors nécessairement V’.
b) Courbes d’analyse thermique :
On peut déduire di diagramme isobare les courbes de refroidissement ou réciproquement.
Application : binaire KCl/NaCl
Un logiciel de simulation fournit le diagramme isobare du chlorure de potassium 1 / chlorure de sodium 2
T= f(x2) en figure 5.
a) On part d’un mélange x2=0.22 à T=750°C. Quel est son état physique ?
b) On effectue un refroidissement isobare. Quelle est la température de solidification commençante ?
Quelle est la composition du premier germe cristallin ?
c) On poursuit le refroidissement jusqu’à 600°C. Dessiner l’allure de la courbe d’analyse thermique
T=f(temps) en précisant les tmpératures de rupture de pente.
d) Même question pour un mélange initial x2=0.49 se refroidissant de 750°C à 600°C.
II) Miscibilité nulle à l’état solide
1)Formation d’un eutectique :
L’immiscibilité totale à l’état solide est le cas le plus fréquent. N’oublions pas que nous supposons toujours
la miscibilité totale à l’état liquide.
a)diagramme isobare :
Prenons l’exemple de deux solides aux caractéristiques physiques assez différentes :
-l’or (noté 1) : Au, système cubique centré,
CT 1064
*
1
;

-le thallium (noté 2) :Th, système quadratique,
CT  5,303
*
2
.
Figure : 6
Partant d’un mélange liquide de composition quelconque (
31  V
, soit sous
atm
P
,V’=2), le
refroidissement peut faire apparaître :
 Soit des cristaux de
S
A1
pur (ou de
S
A2
pur) :
)(1'2 2
l
wfTV 
; cette courbe d’équilibre constitue le liquidus ;
 Soit simultanément des cristaux distincts de
S
A1
et
S
A2
:
 0'3 V
température et composition fixée ; il s’agit du point d’eutexie ( ou du mélange
eutectique : dans notre cas,
CTE131
et
73.0
2
E
w
).
Le point d’eutexie est donc le point triple du diagramme isobare d’équilibre liquide-solides.
Le liquidus est formé par deux portions se coupant au point d’eutexie E. En toute rigueur, le solidus n’est
composé que des portions verticales
0
2w
(
S
A1
pur) et
1
2w
(
S
A2
pur), puisque les deux solides sont
totalement non miscibles.
Réciproquement si nous partons d’un mélange hétérogène quelconque de
SS AA 21 
que nous échauffons, la
fusion ne peut commencer que pour
E
TT 
car le système triphasé impose
0'V
. Le segment de droite
horizontale
E
TT 
représente la limite d’existence du liquide et vient souvent « compléter »le solidus.
Mais en fait le liquide qui apparait a la composition
E
w2
préfixée. Tout point M de ce segment n’est qu’un
point moyen traduisant l’équilibre triphasé de points représentatifs S1 (
S
A1
pur), S2(
S
A2
pur),E(
ll AA 21 
).
Attention : le théorème des moments, précédemment démontré ne s’applique que si deux phases
seulement sont en présence.
La masse de chacune de ces phases varie au cours du changement d’état. Au fur et à mesure que se poursuit
la fusion, le liquide étant plus riche en
l
A2
(car
ME ww 22 
), le mélange hétérogène solide s’enrichit en
S
A1
: