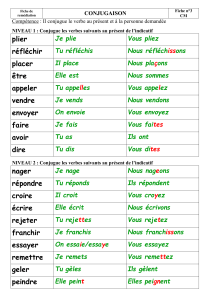
Résumé – Nombres complexes • Définition : L`ensemble des

R´esum´e – Nombres complexes
•D´efinition : L’ensemble des nombres complexes, not´e Cest l’ensemble de tous les nombres de la
forme a+bi, o`u a, b ∈IR, avec i2=−1 :
C={a+bi tels que a, b ∈IR et i2=−1}.
•Partie r´eelle : Si z=a+bi, alors la partie r´eelle de z, not´ee Re(z) est donn´ee par
Re(z) = a.
•Partie imaginaire : Si z=a+bi, alors la partie imaginaire de z, not´ee Im(z) est donn´ee par
Im(z) = b.
•Conjugu´e : Si z=a+bi, alors le conjugu´e de z, not´e ¯zest donn´e par
¯z=a−bi.
Le conjugu´e d’un nombre complexe est donc obtenu en changeant le signe de sa partie imaginaire.
•Addition et Soustraction : Les parties r´eelles et imaginaires sont additionn´ees ou soustraites s´epar´e-
ment. Par exemple, si z1= 3 + 4iet z2= 5 −2i, alors
z1+z2= (3 + 4i) + (5 −2i) = 8 + 2i
et
z1−z2= (3 + 4i)−(5 −2i) = (3 + 4i)+(−5+2i) = −2+6i.
•Multiplication : On effectue les op´erations en traitant icomme une variable symbolique sauf qu’`a
chaque fois qu’on rencontre i2, on le remplace par −1. Par exemple, si z1= 3 + 4iet z2= 5 −2i, alors
z1z2= (3 + 4i)(5 −2i) = 15 + 20i−6i−8i2= 15 + 14i+ 8 = 23 + 14i.
•Division : Pour obtenir z/z2, on multiplie cette fraction par ¯z2/¯z2. Par exemple, si z1= 3 + 4iet
z2= 5 −2i, alors
z1
z2
=z1
z2
¯z2
¯z2
=3+4i
5−2i·5+2i 5+2i=15 + 26i+ 8i2 25 −4i2=15 + 26i−8 25 + 4 =7 + 26i 29 =7 29 +26 29i.
•Remarque : Le produit d’un nombre complexe par son conjugu´e donne toujours un nombre r´eel : si
z=a+bi, alors
z¯z= (a+bi)(a−bi) = a2−b2i2=a2+b2.
•Plan complexe : Un nombre complexe z=a+bi peut ˆetre repr´esent´e par un point dans le plan
complexe. L’axe usuel des xdevient l’axe r´eel tandis que l’axe usuel des ydevient l’axe imaginaire.

•Formes d’un nombre complexe : Un nombre complexe peut prendre l’une des deux formes ci-bas.
•Forme Rectangulaire : C’est la forme que l’on a d´ej`a introduite : z=a+bi.
•Forme Polaire : C’est la forme z=r6θ, o`u le module rest la distance `a l’origine et l’argument
θest l’angle (en degr´es) que fait le segment Oz avec l’axe r´eel.
•Formules de conversion pour passer d’une forme `a l’autre :
•Forme Polaire →Forme Rectangulaire : Soit z=r6θ, alors
a=rcos θet b=rsin θ.
•Forme Rectangulaire →Forme Polaire : Soit z=a+bi, alors
r=pa2+b2.
Pour obtenir θ, on utilisera la convention que −180◦≤θ≤180◦:
θ= tan−1(b/a) + 
0◦,premier ou quatri`eme quadrant,
180◦,deuxi`eme quadrant,
−180◦,troisi`eme quadrant.
•Multiplication et division sous forme polaire : Soient z1=r16θ1et z2=r26θ2, alors
z1z2= (r16θ1)(r26θ2) = r1r26(θ1+θ2).
On remarque que les modules se multiplient et que les arguments s’additionnent. Quant `a la division,
on a
z1
z2
=r16θ1
r26θ2
=r1
r2
6(θ1−θ2).
On remarque que les modules se divisent et que les arguments se soustraient.
•Fonction puissance sous forme polaire : Soit z=r6θ, alors
zn= (r6θ)n=rn6nθ.