Microphone et haut–parleur - CORRECTION PARTIE A : ANALYSE

Thème : Son et musique
Chap. 2 Emetteurs et récepteurs sonores
Microphone et haut-parleur Page 1 / 6 C. Grange-Reynas
Microphone et haut–parleur - CORRECTION
Mots-clefs : Microphone ; enceintes acoustiques.
Contexte du sujet :
Un microphone convertit les ondes sonores en signaux électriques. Un haut-parleur réalise l’opération inverse, il
émet des sons à partir des signaux électriques qu’il reçoit.
Quels sont les points communs entre un microphone et un haut parleur électrodynamiques ?
PARTIE A : ANALYSE ET SYNTHESE DE DOCUMENTS SCIENTIFIQUES
1. Schématiser l’expérience permettant de mettre en évidence la force de Laplace.
2. De quels paramètres dépend le sens de la force de Laplace ? Répondre à cette question en utilisant des
observations expérimentales.
Le sens de la force de Laplace dépend :
 du sens du courant : on intervertit les bornes + et – du générateur, on constate alors qu’il y a
attraction entre la bobine et l’aimant dans un cas et dans l’autre cas, la bobine est repoussée puis
se retourne sur elle-même.
 de l’orientation du champ magnétique crée par l’aimant : on intervertit pôles nord et sud de
l’aimant et on constate le changement de sens de la force de Laplace.
3. Remplacer le générateur de tension continue par un GBF (générateur de tension alternative). Qu’observe-t-
on ?
Pour une fréquence de la tension inférieure à 10 Hz, on remarque que la bobine effectue des allers-retours
vers l’aimant.
Si la fréquence du GBF est trop grande, on ne voit pas bien le mouvement de la bobine.
Autre expérience mettant en évidence la force de Laplace :
http://physiquecollege.free.fr/physique_chimie_college_lycee/lycee/premiere_1S/force_de_laplace
_rail_regle_trois_doigts_main_droite.htm
On emploie la main droite : le pouce = poussée ; index = intensité ; majeur = magnétisme

Thème : Son et musique
Chap. 2 Emetteurs et récepteurs sonores
Microphone et haut-parleur Page 2 / 6 C. Grange-Reynas
4. En argumentant, comparer la directivité du microphone (doc. 2) pour diverses fréquences.
Entre 0 et 60°, la réponse du micro dépend peu de la fréquence.
Le micro capte mieux les sons graves (125 Hz) que les autres, et ce dans toutes les directions.
Le micro capte mal les sons medium (2000 Hz) derrière lui (pour un angle supérieur à 120°).
Le micro capte assez bien les sons aigus (8000 Hz) juste derrière lui (pour un angle proche de 180°).
5. Pourquoi le choix d’un microphone est-il notamment guidé par sa bande passante ?
Un microphone ne capte pas tous les sons de la même façon ; il a une bande passante pour laquelle les sons, dont
la fréquence se situe dans cette gamme, sont captés avec une bonne qualité. Dans le cas du microphone décrit au
document 2, la bande passante est constituée des fréquences comprises entre 100 Hz et 11 kHz environ.
Par exemple, un micro captant mieux les sons graves que les sons aigus sera mieux adapté aux percussions qu’au
violon.

Thème : Son et musique
Chap. 2 Emetteurs et récepteurs sonores
Microphone et haut-parleur Page 3 / 6 C. Grange-Reynas
6. Les graphes ci-contre sont les courbes de réponse en
fréquence de trois haut-parleurs.
Les haut-parleurs de référence DE35, 8PE21 et 12PS100
sont-ils des boomers, des médiums ou des tweeters ?
La bande passante d’un haut-parleur permet de le classer dans les
catégories tweeter, médium ou boomer.
Le DE35 émet mieux les sons aigus de fréquence supérieure à
5 kHz : c’est un tweeter.
Le 12PS100 émet très mal les sons aigus de fréquence supérieure à
3 kHz : c’est un boomer.
Le 8PE21 possède une bande passante large, il émet correctement
les sons de fréquences comprises entre 100 Hz et 5kHz : c’est un
médium.
7. Comparer les rôles d’un microphone et d’un haut-parleur à ceux de l’appareil vocal et de l’oreille humaine.
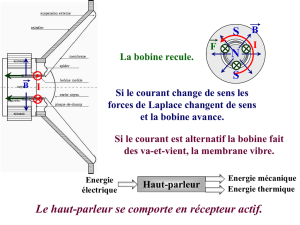
Le haut-parleur a un rôle similaire à l’appareil vocal, il émet du son.
Le microphone capte les sons tout comme l’oreille humaine.
8. Résumer le principe de fonctionnement d’un microphone et d’un haut-parleur électrodynamiques en
précisant les éléments constitutifs communs. Identifier les transferts d’énergie qui ont lieu.
Pour le microphone électrodynamique, les vibrations sonores causent le mouvement d’une membrane et
de la bobine qui lui est solidaire. Grâce au phénomène d’induction électromagnétique, le mouvement de la bobine
placée dans un champ magnétique entraîne l’apparition d’une tension aux bornes du microphone. Cette tension a
une amplitude et une fréquence proportionnelles à celles des vibrations sonores.
L’énergie mécanique du son est transformée en énergie électrique.
Pour le haut-parleur électrodynamique, le principe de fonctionnement est inverse : la tension aux bornes
du haut-parleur met en mouvement une bobine parcourue par un courant. Une membrane solidaire de la bobine
bouge à son tour ce qui permet de créer des vibrations sonores de même fréquence que celle de la tension et dont
l’amplitude varie comme celle de la tension. L’énergie électrique est transformée en énergie mécanique.
Les deux dispositifs possèdent une membrane solidaire d’une bobine, ainsi qu’un aimant créant un champ
magnétique.
Microphone et haut-parleur contiennent 3 éléments communs : une membrane, un aimant et une bobine
de fil conducteur.
Pour le microphone : la membrane vibre sous l’effet du son, elle met en mouvement une bobine créant ainsi une
tension électrique de même fréquence que le son.
Le microphone transforme l’énergie mécanique du son en énergie électrique.
Pour le haut-parleur : Sous l’effet d’une tension électrique, la bobine se met en mouvement entrainant la
membrane qui crée le son.
Le HP transforme l’énergie électrique en énergie mécanique.
Résumé : http://lyc-moulin-st-amand.tice.ac-orleans-tours.fr/eva//sites/lyc-moulin-st-amand/IMG/UserFiles/Flash/phy/hp-mic.swf
Bande passante de trois haut-parleurs

Thème : Son et musique
Chap. 2 Emetteurs et récepteurs sonores
Microphone et haut-parleur Page 4 / 6 C. Grange-Reynas
PARTIE B : RESOLUTION DE PROBLEMES SCIENTIFIQUES
On considère un haut-parleur émettant une onde sonore qui se propage
librement. Le niveau d’intensité sonore mesuré à 1,00 m du haut-
parleur, sur son axe principal, est L1 = 110 dB.
Le diagramme d’émission du haut-parleur est reproduit ci-contre. On le
suppose utilisable pour toutes les fréquences audibles. En un lieu donné,
le niveau d’intensité sonore du son émis par le haut-parleur dépend de
la distance entre ce lieu et le haut-parleur mais aussi de la direction sous
laquelle ce lieu est vu depuis le haut-parleur. Cette direction est repérée
par un angle exprimé en degré.
Pour une distance donnée, ce diagramme permet de connaître la perte
relative du niveau d’intensité sonore en fonction de l’angle par rapport à
l’axe principal du haut-parleur.
Le niveau d’intensité sonore mesuré sur l’axe principal (θ = 0°) constitue la valeur de référence (perte nulle).
Données :
- Niveau d’intensité sonore : L = 10.log 𝐼
𝐼𝑜 en dB.
- Intensité sonore de référence : I0 = 1,0 x10-12 W.m-2.
- L’intensité sonore I à une distance d d’une source émettant dans toutes les directions est liée à la puissance sonore
P de cette source par la relation : I = P / S avec S, la surface de la sphère sonore de rayon d telle que S = 4.π.d2.
- Si x = log(a) alors a = 10x ; log (a x b) = log(a) + log(b)
Problème 1 :
Quel est le niveau d’intensité sonore mesuré à 50 m du haut-parleur dans une direction faisant un angle de 60° avec
l’axe principal du haut-parleur ?
Le niveau d’intensité sonore est donné par la relation : L = 10.log 𝐼
𝐼𝑜
Avec la valeur donnée à 1 m du niveau d’intensité sonore (L1 = 110 dB), on déduit l’intensité sonore I1 à 1 m sur l’axe
principal du haut-parleur : log 𝐼1
𝐼0 = L/10 donc I /I0 = 10(L/10) donc I = I0 x 10(L/10) = 1,0 x10-12 x 10(110/10) = 1,0 x10-1 W.m-2.
On peut en déduire la puissance sonore du haut-parleur : I = P / S
Donc P = I x S
A.N. I = 1,0 x10-1 W.m-2 S = 4 x π x 12 = 12,6 m2 donc P = 1,0 x10-1 x 12,6 donc P = 1,26 W
On cherche l’intensité sonore à la distance d’ = 50 m de la source.
Lorsqu’une source émet de la même façon dans toutes les directions, l’intensité sonore est uniformément répartie
sur une surface sphérique. Cette intensité varie donc comme l’inverse du carré de la distance à laquelle on se trouve
de la source, elle est divisée par quatre lorsque la distance double. I = P / S avec S = 4.π.d2 donc I = P / 4.π.d2
Dans la situation de l’exercice, l’émission n’est pas la même dans toutes les directions. Cependant, dans une
direction donnée, la relation précédente est toujours valable : l’intensité varie comme l’inverse du carré de la
distance.
I’ = P / S

Thème : Son et musique
Chap. 2 Emetteurs et récepteurs sonores
Microphone et haut-parleur Page 5 / 6 C. Grange-Reynas
A.N. P = 1,26 W S = 4 x π x 502 = 31 416 m2
Donc I’ = 1,26 / 31 416 donc I’ = 4,01.10-5 W.m-2
Le niveau d’intensité sonore est donné par la relation : L = 10.log I
Io
Avec la valeur précédemment calculée de I’, on déduit un niveau d’intensité sonore L’ : L = 10.log I′
Io
A.N. I’ = 4,01.10-5 W.m-2 I0 = 1,0 x10-12 W.m-2
Donc L’ = 10 x log (4,01.10-5 / 1,0 x10-12 ) donc L’ = 76 dB
À cette même distance, mais dans une direction faisant un angle de 60° avec l’axe principal, il y a une perte de 6 dB
(voir le diagramme d’émission du hautparleur).
Le niveau d’intensité sonore, à 50 m de la source et dans une direction repérée par θ= 60°, est donc de 70 dB.
Problème 2 :
Montrer que le niveau d’intensité sonore diminue de 6 dB à chaque fois que la distance entre le haut-parleur et le
sonomètre, qui mesure le niveau d’intensité sonore, double.