compte-rendu

Dynamique des vésicules: un modèle pour les
écoulements sanguins ?
L’utilisation de modèles simples permet d’expliquer les phénomènes réels liés aux
mouvements des globules rouges dans le sang.
I) Rappels sur la circulation sanguine.
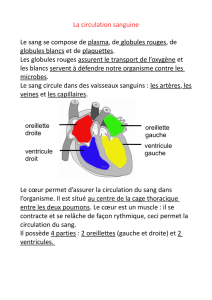
Le sang est un fluide que l’on peut considérer comme newtonien ; il est composé à 45%
d’érythrocytes (globules rouges, diamètre 8!m), de 0,1% de leucocytes (globules blancs) et
de plaquettes.
On s’intéresse ici aux globules rouges, cellules dépourvues de noyau, se déplaçant dans
le circuit capillaire, dont le faible diamètre des canaux est susceptible de provoquer des
bouchons.
On recherche un modèle simple pour décrire un grand nombre de globules rouges dans
un petit espace.
II) Les vésicules.
Peut-on modéliser des globules rouges par des vésicules ?
Un modèle a été proposé par Helfrich en 1973 pour décrire les formes d'équilibre des
vésicules : on considère une vésicule comme une membrane liquide, incompressible et
imperméable.
Le volume et la surface de cette membrane restant constants, on s’intéresse à sa
courbure, caractérisée par une matrice de courbure, de valeurs propres notées c1 et c2, et
on définit :
C=(c1 + c2)/2 et g= c1*c2
L’énergie de courbure est alors donnée par :
K est le module de courbure.
En considérant la membrane comme homogène, le deuxième terme est constant, donc
n’intervient pas dans la recherche des minima d’énergie.
On définit alors le taux de remplissage :
On obtient plusieurs branches d’énergie minimale : la branche prolate, et la branche
oblate ; la branche oblate est caractéristique de la forme des globules rouges :
III) Comparaison avec les propriétés physiques de globules
On compare les modules de compression, de cisaillement et de courbure expérimentaux des
globules rouges avec ceux obtenus par le modèle; puis les coefficients de
compressibilité, de cisaillement et de courbure sous une contrainte de cisaillement :

R est le rayon typique d’un globule rouge.
On constate que le modèle de vésicule est un mauvais modèle expérimental. Les
vésicules sont beaucoup trop flasques pour permettre de décrire correctement des
globules rouges plus rigides.
IV) Propriétés dynamiques.
Pour le réseau capillaire, le nombre de Reynolds vaut 10-3. L’écoulement est donc
visqueux. De plus, les vitesses caractéristiques sont très inférieur à la vitesse du son,
d’où une incompressibilité locale.
Un maillage sur la membrane a été effectué pour connaître les vitesses du fluide sous une
contrainte de cisaillement.
L’expérience montre que l’on a un mouvement en « chenille de char ».
En augmentant le coefficient de cisaillement, la vésicule passe de la branche oblate a la
branche prolate.
Quand le rapport de viscosité augmente, on passe du mouvement de chenille de char, à
un mouvement de roulement de la vésicule sur elle-même.
Il existe une bifurcation entre ces deux types de mouvements : C’est la transition vers le
tumbling.
Conclusion :
Le modèle de vésicule peut aider à la compréhension de écoulements sanguins. C’est un
modèle simple qui présente une grande richesse de comportement. C’est un modèle de
base que l’on peut enrichir en incorporant les effets élastiques, la viscosité de
membrane…