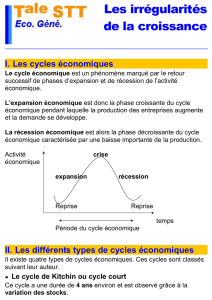
Dans le spectre du quasar 3C 273, la raie spectrale de l`hydrogène

Dans le spectre du quasar 3C 273, la raie spectrale de l’hydrogène,
normalement à 656,1 nm, est à 761,1 nm. Quel était le facteur d’échelle de
l’univers quand la lumière de ce quasar, arrivant à nous aujourd’hui, a été
émise ?
en.wikipedia.org/wiki/3C_273
Découvrez comment résoudre ce problème dans ce chapitre.

Luc Tremblay Collège Mérici, Québec
Version 2016 17 – L’expansion de l’univers 2
La formule
Au début du 20
e
siècle, on commença à mesurer le décalage des raies spectrales des
galaxies dans le but de déterminer leurs vitesses. En 1914, Vesto Slipher annonçait un
résultat assez surprenant. La grande majorité des 12 galaxies qu’il a examinées montre des
spectres décalés vers le rouge. En 1925, il arrivait toujours à cette même conclusion avec
un échantillon comprenant maintenant 40 galaxies. Ces résultats semblaient indiquer que
presque toutes les galaxies s’éloignent de nous. Depuis quelques années, certains
astronomes commençaient à parler d’expansion de l’univers.
C’est aussi en 1925 qu’Edwin Hubble découvrit qu’il y a d’autres galaxies que la Voie
lactée en mesurant la distance de la galaxie d’Andromède. En 1929, Hubble avait ainsi
déterminé la distance de 18 galaxies. En combinant ses résultats avec ceux de Slipher en
1929, Hubble se rend compte qu’il y a un lien entre la distance et le décalage spectral des
galaxies. Ce lien est
zD
où D est la distance de la galaxie. On va faire ici quelque chose ici qui n’est pas correct,
mais qui a été faite à l’époque. On va dire que ce décalage est causé par de l’effet Doppler.
Dans ce cas, cela voudrait dire que le décalage est causé par la galaxie qui s’éloigne de
nous. Ce n’est pas du tout ce qui cause ce décalage, mais la formule qu’on obtiendra avec
cette idée fausse est bonne. On aura l’interprétation correcte de ce résultat plus loin dans
ce chapitre.
Si on suppose que le décalage est dû à l’effet Doppler, on a
vz
et donc que
vzD
vD
Si on note H
0
la constante de proportionnalité, on a
La loi de Hubble
0
vHD
où v est la vitesse d’éloignement de la galaxie. H
0
est la constante de proportionnalité,
appelée le taux d’expansion de Hubble, qui vaut

Luc Tremblay Collège Mérici, Québec
Version 2016 17 – L’expansion de l’univers 3
Taux d’expansion de Hubble.
/
0
67,8 0,9
km s
Mpc
H
On l’appelle parfois la constante de Hubble, mais on va voir que le taux d’expansion varie
avec le temps et que H
0
n’est donc pas une constante.
Notez qu’au départ, Hubble avait obtenu une valeur de la constante beaucoup plus grande,
de l’ordre de 500 km/s/Mpc, parce que l’on confondait deux types de céphéides à cette
époque. L’erreur ne sera corrigée qu’en 1952.
La relation entre la vitesse et la distance n’est pas parfaite. Voici un graphique montrant la
vitesse en fonction de la distance pour 1355 galaxies.
hendrix2.uoregon.edu/~imamura/123/lecture-1/xpand.html
On voit que les points ne forment pas une droite parfaite. La loi de Hubble est plutôt une
tendance. Une partie de cette dispersion vient de l’incertitude sur la distance des galaxies,
mais ce n’est pas la seule explication. Nous verrons l’explication complète un peu plus
loin.
Exemple 17.1.1
Quelle est la vitesse d’éloignement de la
galaxie du Sombréro, située à une
distance de 29,3 millions d’années-
lumière selon la loi de Hubble ?
en.wikipedia.org/wiki/File:M104_ngc4594_sombrero_galaxy_hi-res.jpg

Luc Tremblay Collège Mérici, Québec
Version 2016 17 – L’expansion de l’univers 4
La distance de cette galaxie, en Mpc est,
1
29,3 8,98
3, 262
pc
D
Mal Mpc
al
La vitesse d’éloignement selon la loi de Hubble est donc
/
67,8 8,98
609
km s
Mpc
km
s
vMpc
(La véritable vitesse d’éloignement de cette galaxie est de 1024 km/s.)
Distance des galaxies très éloignées
Pour des galaxies très éloignées (plus de 1 milliard d’années-lumière), il est difficile de
voir les céphéides et de mesurer la vitesse de rotation de la galaxie. On peut toujours trouver
la distance s’il y a une supernova de type Ia dans la galaxie, mais ces évènements sont
plutôt rares.
Dans ce cas, on utilise la loi de Hubble pour trouver la distance de ces galaxies très
éloignées.
Exemple 17.1.2
Une galaxie s’éloigne de nous à 20 000 km/s. Quelle est la distance de cette galaxie ?
La distance de la galaxie est
0
/
20000 67,8
295 962
km ks s
sMpc
vHD
D
DMpcMal
Évidemment, la distance trouvée par la loi de Hubble reste assez approximative.
Retour sur les quasars
C’est exactement ce genre de calcul qui laissait croire que les quasars étaient très éloignés
de la Terre. Quand on fit le spectre des premiers quasars au début des années 1960, on
obtint des résultats surprenants. Personne ne reconnaissait les raies d’émission ou
d’absorption du spectre ! En 1963, Maarten Schmidt se rend compte que ces spectres sont
tout simplement très décalés vers le rouge. Par exemple, le spectre du quasar 3C 273 est

Luc Tremblay Collège Mérici, Québec
Version 2016 17 – L’expansion de l’univers 5
décalé de 16 % (les longueurs d’onde sont 16 % plus grandes que les valeurs de longueurs
d’onde normales), ce qui veut dire que la galaxie s’éloigne de nous rapidement.
frigg.physastro.mnsu.edu/~eskridge/astr101/kauf27_4.JPG
C’est cette vitesse d’éloignement importante qui laissait croire que les quasars étaient très
loin de la Terre selon la loi de Hubble, ce qui fut confirmé par la suite.
En réalité, ce décalage des raies est bel et bien relié à la distance de la galaxie, mais il n’est
pas dû à l’effet Doppler se produisant parce que la galaxie s’éloigne de nous. On verra un
peu plus loin l’interprétation correcte du décalage selon la relativité générale.
Une vitesse proportionnelle à la distance indique que l’univers est en expansion.
Pour montrer cela, imaginons trois galaxies A, B et C à certaines distances les unes des
autres. Imaginons ensuite que l’univers prend lentement de l’expansion, de sorte que les
distances sont toutes augmentées de 10 % au bout d’un certain temps T.