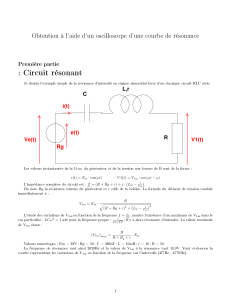
: Circuit résonant Première partie

Obtention à l'aide d'un oscilloscope d'une courbe de résonance
Première partie
: Circuit résonant
Je choisis l'exemple simple de la résonance d'intensité en régime sinusoïdal forcé d'un classique circuit RLC série.
L,r
C
i(t)
e(t)
R
Ve(t)
V1(t)
Rg
Les valeurs instantanées de la f.é.m. du générateur et de la tension aux bornes de R sont de la forme :
e(t) = Em · cos(ωt)
V 1(t) = V1m · cos (ωt − ϕ)
1
L'impédance complexe du circuit est : Z = (R + Rg + r) + j · Lω − Cω
.
On note Rg la résistance interne du générateur et r celle de la bobine. La formule du diviseur de tension conduit
immédiatement à :
R
V1m = Em · q
2
(R + Rg + r) + Lω −
1 2
Cω
ω
L'étude des variations de V1m en fonction de la fréquence f = 2π
, montre l'existence d'un maximum de V1m dans le
1
2
cas particulier : LCω = 1 soit pour la fréquence propre : 2π√LC ; il y a alors résonance d'intensité. La valeur maximale
de V1m étant :
(V1m )max =
R
· Em
R + Rg + r
Valeurs numériques : Em = 22V ; Rg = 50 ; C = 369nF ; L = 10mH ; r = 10 ; R = 50.
La fréquence de résonance vaut ainsi 2620Hz et la valeur de V1m à la résonance vaut 10,0V. Voici ci-dessous la
courbe représentant les variations de V1m en fonction de la fréquence sur l'intervalle [477Hz , 4770Hz].
1
ser
Deuxième partie
: Montage suiveur à amplicateur opérationnel
parfait (AOP 1).
C
L,r
i(t)
ie=0
i(t)
e(t)
R
Ve(t)
ε1
E+
AOP1
E−
S
V1(t)
Rg
S1(t)
Remarque : l'amplicateur opérationnel est aussi appelé Amplicateur linéaire intégré.
Étape n° 1 : observation des liaisons entrées - sortie.
Nous constatons l'existence d'une liaison par conducteur entre l'entrée inverseuse E- et la sortie S ainsi que l'absence de liaison entre l'entrée non inverseuse E+ et la sortie S.
Nous pouvons considérer que, sous réserve d'une amplitude trop grande de V1(t), l'AOP fonctionne en régime linéaire.
Remarque : cette observation préliminaire est très importante : imaginons une permutation des entrées E+ et E- :
le régime linéaire deviendrait alors impossible : la situation ε1 = 0 serait une situation instable ; le fonctionnement de
l'AOP serait radicalement diérent.
De façon évidente :
Étape n° 2 : expressions des tensions d'entrées.
VE+ = V 1(t)
Étape n° 3 : régime linéaire de l'AOP.
VE− = S1(t)
Dans ce cas : ε1 = 0 ; VE+ = VE− .Cela conduit à :
S1(t) = V 1(t) ∀t
L'AOP fonctionne en suiveur de tension.
2
Intérêt de ce suiveur : supposons que l'on supprime l'AOP en branchant directement la partie droite du
montage directement aux bornes de la résistance R. On aurait encore S1(t) = V 1(t) ∀t mais l'intensité ie ne serait pas
nulle ; R ne serait pas parcourue par le même courant que le condensateur et la bobine : le branchement de la partie
droite du circuit perturberait le fonctionnement du circuit RLC.
Troisième partie
: Montage redresseur mono-alternance à diode idéale.
L,r
C
Ud
i(t)
ie=0
i(t)
e(t)
ε1
R
Ve(t)
AOP1
E+
i2(t)
S
E−
R2
V1(t)
Rg
V2(t)
S1(t)
Deux cas de fonctionnement de la diode sont envisageables :
Premier cas : la diode est conductrice : i2(t) > 0 ; la loi d'Ohm conduit à : V 2(t) = R2 · i2(t) > 0.
De plus : S1(t) = U d + V 2(t) . La diode est idéale : U d = 0.
Conclusion : lorsque la diode conduit : V 2(t) = S1(t) mais cela n'est possible que si : S1(t) > 0.
Second cas : la diode ne conduit pas (état bloquée) :i2(t) = 0 ; V 2(t) = R2 · i2(t) = 0.
De plus : S1(t) = U d + V 2(t) = U d . La diode est idéale : U d < 0 ; donc : S1(t) < 0.
Conclusion : la diode est bloquée lorsque S1(t) < 0 et alors : V 2(t) = 0.
Synthèse : l'ensemble {diode idéale, résistance R2} se comporte en redresseur mono-alternance :
V 2(t) = S1(t) si S1(t) ≥ 0
V 2(t) = 0
si S1(t) < 0
Quatrième partie
: ltre passe-bas du premier ordre.
C
L,r
Ud
i(t)
ie=0
i(t)
e(t)
Ve(t)
ε1
E+
E−
AOP1
i2(t)
S
AOP2
E+
R3
E−
R
R2
V1(t)
Rg
S1(t)
C3
V2(t)
S2(t)
V3(t)
L'AOP n°2 fonctionne en suiveur. Nous obtenons ainsi :
S2(t) = V 2(t) ∀t
Si la résistance R3 était directement reliée à la sortie de la diode, la diode et R2 ne serait plus parcourues par
le même courant, ce qui perturberait le fonctionnement du redresseur. La tension V3(t) est appliquée à l'entrée d'un
oscilloscope dont l'impédance est supposée très grande devant R3 ; on peut donc négliger le courant dans la branche de
C3 et ainsi considérer que R3 et C3 se comportent en diviseur de tension. Supposons pour commencer que S2(t) soit
une tension sinusoïdale. En utilisant les complexes associés aux tensions instantanées, on obtient :
3
V 3 = S2 ·
1
jC3 ω
R3 +
1
jC3 ω
=
S2
1 + jR3 C3 ω
En passant aux amplitudes des tensions sinusoïdales :
V3m = q
S3m
2
1 + (R3 C3 ω)
Considérons maintenant une tension sinusoïdale redressée mono-alternance d'amplitude S3m=V2m :
T
S3m (t) = V2m · sin( 2π
T t) tant que V 2(t) > 0 c'est à dire tant que : 0 < t < 2 ;
T
S3m (t) = 0 tant que V 2(t) ≤ 0 c'est à dire tant que : 2 ≤ t ≤ T .
La composante continue de cette tension est sa valeur moyenne :
1
V2 =
T
ˆ
T
0
V2m
V 2(t) · dt =
T
ˆ
T
2
sin
0
T2
2π
V2m T
2π
V2m
t dt =
·
· − cos
t
=
T
T
2π
T
π
0
Le théorème de Fourier permet d'écrire la tension sinusoïdale redressée mono-alternance sous la forme :
∞
S2(t) = V 2(t) =
V2m X
+
Am · cos (nωt + ϕn )
π
n=1
Examinons l'action du ltre passe-bas sur chaque composante de cette tension :
- action sur la composante continue : c'est le cas limite d'une tension de pulsation nulle ; la composante continue est
donc conservée.
3
- action sur les composantes sinusoïdales : dans cette étude, nω ≥ 2π · 477≈ 3.10
q rad/s ; en choisissant R3=100k ;
C3=200nF, pour toutes les fréquences des composantes sinusoïdales, nous avons : 1 + (R3 C3 nω)2 >> 1. Les composantes sinusoïdales de V2(t) sont donc extrêmement atténuées au point de devenir négligeables devant la composante
continue.
Conclusion : nous obtenons une tension de sortie V3 pratiquement constante et égale à :
V3=
V2m
π
Finalement, l'ensemble du montage, alimenté sous tension sinusoïdale, fournit en sortie une tension
quasi continue, proportionnelle à l'amplitude de V1(t), c'est à dire aussi proportionnelle à l'amplitude
de l'intensité i(t).
Cinquième partie
: Vobulation : obtention à l'oscilloscope de la courbe
de résonance d'intensité.
Nous remplaçons maintenant le générateur de tension par un vobulateur : il s'agit d'un générateur dont la f.é.m. e(t)
est une fonction sinusoïdale de temps d'amplitude Em constante (22V) dont la fréquence varie linéairement en fonction
du temps de manière très lente, c'est à dire que la durée nécessaire pour passer de la fréquence minimale à la fréquence
maximale est très grande devant la période moyenne : ici la durée de balayage est de 1s alors que la période moyenne
est de 4,4.10-4 s. En 1s, la fréquence augmente linéairement de 477Hz à 4770Hz selon la loi :
f = 477 + 4293 · t
Sur chaque période de tension, la variation de fréquence est extrêmement faible de sorte que les résultats démontrés
au dessus pour des tensions de fréquence xe s'applique en très bonne approximation. Voici, pour s'en convaincre les
résultats obtenus pour t compris entre 496ms et 504ms, la fréquence variant faiblement sur ce faible intervalle de temps
autour de la fréquence de résonance.
4
On peut facilement vérier les résultats théoriques démontrés. Supposons maintenant que la largeur de l'écran de
l'oscilloscope corresponde à 1s : les courbes vont être extrêmement resserrées. Voici ci-dessous le résultat obtenu pour
V1(t) :
Voici maintenant le résultat pour V2(t) : la partie négative a disparue :
5
Voici maintenant le résultat obtenue pour V3(t) :
Connaissant la relation entre t et f, il serait en fait possible de graduer l'axe horizontale en hertz. L'ordonnée
représente l'amplitude de V1(t) divisé par . À un facteur d'échelle près, nous obtenons bien la courbe de
résonance d'intensité du circuit RLC.
6