Fiche d`exercices 4

1/3
Sup PCSI 6
Année 2011/2012
Fiche d'exercices 3
Miroirs sphériques
1. Construction d’un rayon quelconque :
On considère un miroir sphérique utilisé dans les conditions de Gauss. On note C son centre, S son
sommet, et F son foyer. Construire graphiquement la marche d’un rayon lumineux après réflexion sur le
miroir de quatre manières différentes :
a. en utilisant le centre C et le plan focal objet.
b. en utilisant le centre C et le plan focal image.
c. en utilisant le sommet S et le plan focal objet.
d. en utilisant le sommet S et le plan focal image.
On étudiera séparément les deux cas concernant un miroir concave et un miroir convexe.
2. Miroir convexe :
Soit un miroir convexe, de sommet S, de centre C, utilisé dans l'approximation de Gauss, de rayon
R
SC
(figure 1)
C
S
AA' x
Figure 1
a) Expliquer ce qu'est l'approximation de Gauss.
b) Rappeler les formules de conjugaison du miroir avec origine au sommet reliant la position d'un point
objet A de l'axe Sx à son image A'. On posera x =
SA
et x' =
SA'
.
c) Placer les foyers. Exprimer la vergence en fonction de R. En quelle unité exprime-t-on la vergence ?
d) Soit un objet à l'infini, centré sur l'axe du miroir, vu sous un angle  ; déterminer son image à travers
le miroir : position, taille, nature de l'image ; la construire.
Application numérique : on donne  = 2,0 secondes d'arc et R = 4,46 m. Déterminer la taille de l'image.
3. Observation d’un miroir éclairé :
Une source modélisée par un disque lumineux de centre A et de diamètre BD = 2 cm, est placée devant
un miroir sphérique concave de rayon de courbure R = 30 cm, de rayon d’ouverture r = 6 cm, de centre C,
de sommet S et de foyer F.
Oeil
r
B
D
A
d

2/3
a. La source est placée au milieu de FC. Construire, puis préciser la position et la taille de l’image de la
source donnée par le miroir sphérique.
b. Reprendre cette étude dans le cas où la source est placée au milieu de SF.
4. Détermination des caractéristiques d’un miroir sphérique :
a. Quelles sont les caractéristiques d’un miroir sphérique qui donne d’un objet réel placé à 60 cm de son
sommet une image droite et réduite d’un rapport 5 ?
b. Même question si l’objet étant toujours placé à 60 cm du sommet du miroir, l’image est inversée et
agrandie dans un rapport 5.
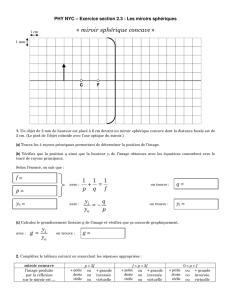
5. Le rétroviseur :
Un rétroviseur est assimilable à un miroir sphérique convexe de vergence V = + 2,0 .
a. Préciser la position de l’image d’un objet situé à 20 m du miroir et le grandissement.
b. Ce rétroviseur est observé par l’œil du conducteur placé à d = 1,0 m, et il est diaphragmé par un cercle
de rayon r = 6,0 cm (taille du rétroviseur). Calculer la hauteur maximale d’un camion situé sur la route à 20
m du rétroviseur telle que le conducteur voie le camion entièrement.
6. Association de deux miroirs sphériques :
1. Par définition, un miroir sphérique est constitué par une surface réfléchissante en forme de calotte
sphérique. L’axe de symétrie de cette calotte est appelé axe optique principal. Cet axe passe par le centre C
du miroir et « perce » celui-ci en son sommet S.
1.a. Faire les schémas de miroirs concaves et convexes avec leurs foyers
1.b. Un miroir concave est-il convergent ou divergent ? Et un miroir convexe ? Faire les schémas
correspondants.
2. On réalise un système optique constitué par l’association de deux miroirs sphériques M1 (concave,
sommet S1, centre C1, rayon R1) et M2 (convexe, sommet S2, centre C2, rayon R2) de même axe optique
principal, disposés comme sur la figure ci-dessous :
Le miroir M1 est percé en son sommet S1 d’un petit trou permettant à la lumière de passer, mais ne
modifiant pas ses propriétés. Les distances focales f1 et f2 des deux miroirs M1 et M2 sont telles que
mf 0,3
1
et
mf 0,2
2
.
2.a. On note
12SSd 
.
Déterminer d pour que tout rayon incident parallèle à l’axe optique et réfléchi par les deux miroirs passe par
S1. Vérifier le calcul par un graphique à l’échelle de 2 cm pour 1 m. Dans la suite, on conservera cette valeur
de d.
2.b. Déterminer la position des foyers F et F’ de ce système optique.
C2
S2
C1
S1

3/3
L'ensemble constitue l'objectif d'un télescope (Pic du Midi), monté en "Cassegrain" et permet d’observer
des objets situés à l’infini.
2.c. Soit un objet lumineux, ponctuel, à l'infini sur l'axe ; déterminer son image après réflexion des
rayons lumineux sur M1 puis sur M2.
2.d. Soit un objet lumineux, étendu, à l'infini, de diamètre apparent . Déterminer son image (position,
taille, nature de l'image) ; la construire.
Application numérique :  = 2 secondes d'arc.
Eléments de réponse :
2. d. image droite, virtuelle, de taille 2,2 10-5 m, avec SA’=R/2.
3. a.
2/' RCA 
; B’D’ = 4 cm b.
2/3' RCA 
; B’D’ = 4 cm
4. a. f = 15 cm b. f = -50 cm
5. a. gt = 0,024 b.
t
g
r
dfd
H'
max
; AN : Hmax = 3,75 m
6. 2.a. d = 2 m 2.b.
mFS 12
1
; F’ = S1 2.c. A’=F’
2.d. image renversée, réelle, de taille 5,8 10-5 m, située en S1.