Pratiquer l’algorithmique Qu’est-ce qu’un algorithme ? THÈME 1

1
Enseignement spécifique ● Pratiquer l'algorithmique
© Nathan 2012 – Transmath Term. S
Pratiquer
l’algorithmique
THÈME 1
Qu’est-ce qu’un algorithme ?
Activité
2 – Tracé d’au moins deux hauteurs issues des sommets
du triangle.
– Tracé du point H, intersection des hauteurs tracées.
3 Traitement : le tracé des hauteurs.
Exercices
1 1. Les points O et A.
2. Un carré de centre O et dont un sommet est A.
2 Éléments donnés : l’expression de f (x) et la valeur a.
Question posée : « Donnez l’équation de la tangente à la
courbe représentant f au point d’abscisse a.
3 Entrées : les coefficients A, B et C du trinôme.
Traitements : le calcul du discriminant DELTA.
Sorties : les valeurs a et b.
4 1. On peut déduire le sens de variation de la fonction
f sur l’intervalle I.
2. b)
f ’ est positive pour x  −1 et pour x  2. Donc la fonction
f est strictement croissante sur ]–  ; −1] et [2 ; + [ et stric-
tement décroissante sur [−1 ; 2].
5 Les entrées de ces deux algorithmes ne sont pas
identiques. On ne peut donc pas dire que ces algorithmes
sont équivalents.
6 • Créez dans l’ordre : le triangle ABC, deux
bissectrices intérieures à ce triangle, le point d’intersection D
des deux bissectrices, la perpendiculaire à l’un des côtés
passant par le point D, le point d’intersection E entre cette
perpendiculaire et le côté utilisé, le cercle de centre D
passant par E.
• Utilisez la commande « Créer un nouvel outil ».
• Choisissez le cercle inscrit dans l’onglet « objets finaux »,
les points A, B et C dans l’onglet « objets initiaux ».

2Enseignement spécifique ● Pratiquer l'algorithmique
© Nathan 2012 – Transmath Term. S
b) Oui. Voir la question 2.
2. Avec AlgoBox :
11 1. p, n, t, PHT et PTTC.
2. PHT PREND_LA_VALEUR n*p
PTTC PREND_LA_VALEUR PHT*(1+t/100)
3. a) p, n, t.
b) p PREND_LA_VALEUR n*p
p PREND_LA_VALEUR p*(1+t/100)
c) L’économie du nombre de variables dégrade la lisibilité
de l’algorithme.
Activité
1 On obtient f (4).
2 5 – 3 EXE ÷ – 2 EXE
Exercices
7 5 × 5 + 4 × 4 EXE EXE
8 a) 4 A EXE A – 2
B EXE A × B + 5 EXE
b) 4 + 2 A EXE 2 – 5 ÷ A EXE
9 A – 2 ; B – 3 ; C – 1.
10 1. a) On peut envisager jusqu’à cinq variables :
le premier nombre A, le carré B de ce premier nombre,
le second nombre C, le carré D de ce second nombre, la
somme E de B et D.
THÈME 3
L’instruction conditionnelle
Activité
Exercices
12 T.I.
Casio
13 1. Il suffit d’ajouter une variable p et la ligne de
traitement « p prend la valeur b-m*a ».
2. Avec AlgoBox :
1 VARIABLES
2 a EST_DU_TYPE NOMBRE
3 b EST_DU_TYPE NOMBRE
4 c EST_DU_TYPE NOMBRE
5 d EST_DU_TYPE NOMBRE
6 m EST_DU_TYPE NOMBRE
7 p EST_DU_TYPE NOMBRE
8 DEBUT_ALGORITHME
9 AFFICHER «Saisissez les coordonnées
du point A.»
10 LIRE a
11 LIRE b
12 AFFICHER «Saisissez les coordonnées
du point B.»
13 LIRE c
14 LIRE d
15 //
On calcule les paramètres de la
droite
16 m PREND_LA_VALEUR (d-b)/(c-a)
17 AFFICHER «Le coefficient directeur
de (AB) est »
18 AFFICHER m
19 p PREND_LA_VALEUR b-m*a
20 AFFICHER «L’ordonnée à l’origine
de (AB) est »
21 AFFICHER p
22 FIN_ALGORITHME
THÈME 2
Variables et affectation

3
Enseignement spécifique ● Pratiquer l'algorithmique
© Nathan 2012 – Transmath Term. S
3. Avec AlgoBox :
1 VARIABLES
2 a EST_DU_TYPE NOMBRE
3 b EST_DU_TYPE NOMBRE
4 c EST_DU_TYPE NOMBRE
5 d EST_DU_TYPE NOMBRE
6 m EST_DU_TYPE NOMBRE
7 p EST_DU_TYPE NOMBRE
8 DEBUT_ALGORITHME
9 AFFICHER «Saisissez les coordonnées
du point A.»
10 LIRE a
11 LIRE b
12 AFFICHER «Saisissez les coordonnées
du point B.»
13 LIRE c
14 LIRE d
15 SI (a==c) ALORS
16 DEBUT_SI
17 AFFICHER «(AB) est parallèle à (Oy)
et a pour équation x = »
18 AFFICHER a
19 FIN_SI
20 SINON
21 DEBUT_SINON
22 m PREND_LA_VALEUR (d-b)/(c-a)
23 AFFICHER «Le coefficient directeur
de (AB) est »
24 AFFICHER m
25 p PREND_LA_VALEUR b-m*a
26 AFFICHER «L’ordonnée à l’origine
de (AB) est »
27 AFFICHER p
28 FIN_SINON
29 FIN_ALGORITHME
14 a) Cet algorithme teste la colinéarité ou l’ortho-
gonalité de deux vecteurs définis par leurs coordonnées.
Ligne 15 : « … colinéaires. »
Ligne 19 : « … orthogonaux. »
b) et c) Le programme AlgoBox final peut être :
1 VARIABLES
2 a EST_DU_TYPE NOMBRE
3 b EST_DU_TYPE NOMBRE
4 c EST_DU_TYPE NOMBRE
5 d EST_DU_TYPE NOMBRE
6 k EST_DU_TYPE NOMBRE
7 message EST_DU_TYPE CHAINE
8 DEBUT_ALGORITHME
9 AFFICHER «Entrez les coordonnées du
vecteur u.»
10 LIRE a
11 LIRE b
12 AFFICHER «Entrez les coordonnées du
vecteur v.»
13 LIRE c
14 LIRE d
15 SI (a==0 et b==0) ALORS
16 DEBUT_SI
17 AFFICHER «u est nul.»
18 FIN_SI
19 SI (c==0 et d==0) ALORS
20 DEBUT_SI
21 AFFICHER «v est nul.»
22 message PREND_LA_VALEUR «v= 0 u.»
23 FIN_SI
24 SINON
25 DEBUT_SINON
26 SI (c==0) ALORS
27 DEBUT_SI
28 k PREND_LA_VALEUR b/d
29 message PREND_LA_VALEUR
«u = «+k+» v.»
30 FIN_SI
31 SINON
32 DEBUT_SINON
33 k PREND_LA_VALEUR a/c
34 message PREND_LA_VALEUR
«u = «+k+» v.»
35 FIN_SINON
36 FIN_SINON
37 SI (a*d-b*c==0) ALORS
38 DEBUT_SI
39 AFFICHER «u et v sont colinéaires.»
40 AFFICHER message
41 FIN_SI
42 SI (a*c+b*d==0) ALORS
43 DEBUT_SI
44 AFFICHER «u et v sont orthogonaux.»
45 FIN_SI
46 FIN_ALGORITHME
15 T.I.
Casio
16 1.
Entrées Sorties
A B C A B H
487478
874478
847748
478478

4Enseignement spécifique ● Pratiquer l'algorithmique
© Nathan 2012 – Transmath Term. S
THÈME 4
La boucle conditionnelle
Activité
4 Le dixième carré a un côté inférieur à 0,5.
Exercices
17 1. et 2.
T.I.
Casio
Remarque. Dans le langage de programmation CASIO, les
instructions d’une boucle « Do-LpWhile » sont exécutées
une première fois, puis tant que la condition est vérifiée.
18 1. Au début du jeu, le lièvre et la tortue sont derrière
la ligne de départ. Un dé est lancé. Si le résultat de ce
lancer est 6, alors le lièvre arrive directement sur la case
« Arrivée » et remporte la manche. Sinon, la tortue avance
d’un nombre de cases égal au résultat du lancer. Si la tortue
arrive sur la case « Arrivée », alors elle remporte la manche.
On relance le dé jusqu’à ce que l’un des protagonistes
remporte la manche.
2. Avec AlgoBox :
1 VARIABLES
2 T EST_DU_TYPE NOMBRE
3 L EST_DU_TYPE NOMBRE
4 D EST_DU_TYPE NOMBRE
5 GL EST_DU_TYPE NOMBRE
6 GT EST_DU_TYPE NOMBRE
7 i EST_DU_TYPE NOMBRE
8 DEBUT_ALGORITHME
9 i PREND_LA_VALEUR 0
10 GT PREND_LA_VALEUR 0
11 GL PREND_LA_VALEUR 0
12 TANT_QUE (i<1000) FAIRE
13 DEBUT_TANT_QUE
14 i PREND_LA_VALEUR i+1
15 D PREND_LA_VALEUR 0
16 T PREND_LA_VALEUR 0
17 L PREND_LA_VALEUR 0
18 TANT_QUE (T<7 ET L!=7) FAIRE
19 DEBUT_TANT_QUE
20 SI (D==6) ALORS
21 DEBUT_SI
22 L PREND_LA_VALEUR 7
23 GL PREND_LA_VALEUR GL+1
24 FIN_SI
25 SINON
26 DEBUT_SINON
27 T PREND_LA_VALEUR T+D
28 FIN_SINON
29 SI (T>=7) ALORS
30 DEBUT_SI
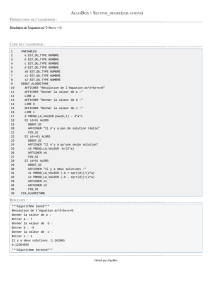
2. Cet algorithme affecte à la variable H la plus grande des
valeurs A, B, C initialement saisies.
Avec AlgoBox :
1 VARIABLES
2 a EST_DU_TYPE NOMBRE
3 b EST_DU_TYPE NOMBRE
4 c EST_DU_TYPE NOMBRE
5 h EST_DU_TYPE NOMBRE
6 DEBUT_ALGORITHME
7 LIRE a
8 LIRE b
9 LIRE c
10 h PREND_LA_VALEUR c
11 SI (a<b) ALORS
12 DEBUT_SI
13 SI (b>c) ALORS
14 DEBUT_SI
15 h PREND_LA_VALEUR b
16 b PREND_LA_VALEUR c
17 FIN_SI
18 FIN_SI
19 SINON
20 DEBUT_SINON
21 SI (a>c) ALORS
22 DEBUT_SI
23 h PREND_LA_VALEUR a
24 a PREND_LA_VALEUR c
25 FIN_SI
26 FIN_SINON
27 SI (h*h==a*a+b*b) ALORS
28 DEBUT_SI
29 AFFICHER «Le triangle est rectangle.»
30 FIN_SI
31 SINON
32 DEBUT_SINON
33 AFFICHER «Le triangle n’est pas
rectangle.»
34 FIN_SINON
35 FIN_ALGORITHME

5
Enseignement spécifique ● Pratiquer l'algorithmique
© Nathan 2012 – Transmath Term. S
19 1. Avec AlgoBox :
1 VARIABLES
2 u EST_DU_TYPE NOMBRE
3 v EST_DU_TYPE NOMBRE
4 a EST_DU_TYPE NOMBRE
5 b EST_DU_TYPE NOMBRE
6 p EST_DU_TYPE NOMBRE
7 DEBUT_ALGORITHME
8 u PREND_LA_VALEUR 2
9 v PREND_LA_VALEUR 1
10 LIRE p
11 TANT_QUE (u-v>p) FAIRE
12 DEBUT_TANT_QUE
13 a PREND_LA_VALEUR (u+v)/2
14 b PREND_LA_VALEUR 4/(u+v)
15 u PREND_LA_VALEUR a
16 v PREND_LA_VALEUR b
17 FIN_TANT_QUE
18 AFFICHER v
19 AFFICHER u
20 FIN_ALGORITHME
2. On modifie les lignes suivantes :
8 u PREND_LA_VALEUR 5
14 b PREND_LA_VALEUR 10/(u+v)
20 1. Selon les habitudes de programmation, les répon ses
peuvent être variées.
Voici un algorithme utilisant les opérateurs de base :
Variables
a, b et c sont de type numérique
Entrée
Lire a et b
Tant que a>0
R prend la valeur a
a prend la valeur a-b
Fin de boucle
Sortie
Afficher R
2. La structure « jusqu’à » n’existe pas pour tous les langages
de programmation. On utilise alors une structure « tant que »
en s’assurant que les instructions de la boucle seront exécu-
tées au moins une fois. Exemple avec AlgoBox :
3. PGCD(660 ; 1 050) = 30 et PGCD(4 410 ; 2 100) = 210.
31 GT PREND_LA_VALEUR GT+1
32 FIN_SI
33 D PREND_LA_VALEUR ALGOBOX_ALEA_
ENT(1,6)
34 FIN_TANT_QUE
35 FIN_TANT_QUE
36 AFFICHER « Nombre de parties gagnées
par le lièvre : »
37 AFFICHER GL
38 AFFICHER « Nombre de parties gagnées
par la tortue : »
39 AFFICHER GT
40 FIN_ALGORITHME
3.
1 VARIABLES
2 T EST_DU_TYPE NOMBRE
3 L EST_DU_TYPE NOMBRE
4 D EST_DU_TYPE NOMBRE
5 GL EST_DU_TYPE NOMBRE
6 GT EST_DU_TYPE NOMBRE
7 gagnant EST_DU_TYPE CHAINE
8 DEBUT_ALGORITHME
9 //
La tortue et le lièvre sont derrière
la ligne de départ.
10 T PREND_LA_VALEUR 0
11 D PREND_LA_VALEUR 0
12 TANT_QUE (T<7 ET L!=7) FAIRE
13 DEBUT_TANT_QUE
14 //
On lance un dé tant qu’il n’y a
pas de vainqueur.
15 D PREND_LA_VALEUR ALGOBOX_ALEA ENT(1,6)
16 AFFICHER D
17 //
Si le dé indique 6 alors le
lièvre arrive directement sur la
case arrivée et gagne la partie.
18 SI (D==6) ALORS
19 DEBUT_SI
20 L PREND_LA_VALEUR 7
21 gagnant PREND_LA_VALEUR «le lièvre.»
22 FIN_SI
23 SINON
24 DEBUT_SINON
25
//Sinon la tortue avance du
nombre de cases indiquées par le
dé.
26 T PREND_LA_VALEUR T+D
27 FIN_SINON
28 SI (T>=7) ALORS
29 DEBUT_SI
30
//Si la tortue franchit la ligne
d’arrivée alors elle gagne la
partie.
31 gagnant PREND_LA_VALEUR «la tortue.»
32 FIN_SI
33 FIN_TANT_QUE
34 AFFICHER «Le gagnant est : »
35 AFFICHER gagnant
36 FIN_ALGORITHME
4. La tortue semble avantagée. En modifiant le programme,
on peut conjecturer que pour 10 ou 11 cases, le jeu est plus
équitable.