1 - Cours2Mat

5 - Quadrilatères particuliers

Chap5 - Quadrilatères particuliers
I –Les quadrilatères particuliers
Quadri latère
==
4côtés
Un quadrilatère particulier est une figure qui a:
4 côtés
et une particularité (quelque chose en plus)
Les quadrilatères particuliers connus sont:
•Trapèze
•Parallélogramme
•Losange
•Rectangle
•Carré

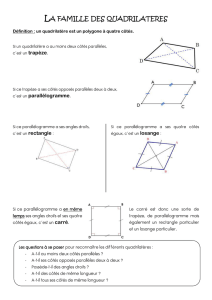
a) Le Trapèze
Un trapèze est un quadrilatère qui a :
2 côtés parallèles ( 1 paire de côtés parallèles)
b) Le Parallélogramme
Le parallélogramme est un quadrilatère qui a:
1) Ses côtés opposés parallèles ( 2 paires de côtés parallèles)
2) Ses côtés opposés égaux
3) Des diagonales de même milieu
Remarque: Le trapèze est-il un parallélogramme? Le parallélogramme est-il un trapèze?
Le trapèze n’est pas un parallélogramme puisqu’il n’a que 2 côtés parallèles.
Le parallélogramme est un trapèze puisqu’il a bien 1 paire de côtés parallèles.
1) 2) 3)

c) Le Losange
Un losange est un quadrilatère qui a :
4 côtés égaux
Remarque:
Le losange est un parallélogramme car il a bien ses côtés opposés égaux.
Propriétés:
Comme les parallélogrammes +
Les diagonales du losange sont perpendiculaires.

d) Le Rectangle
Le rectangle est un quadrilatère qui a:
3 angles droits (donc 4)
Remarque:
Le rectangle est un parallélogramme car il a bien ses côtés opposés parallèles.
Propriétés:
Comme les parallélogrammes +
Les diagonales du rectangle ont la même longueur.
e) Le carré :
Le carré est un rectangle et un losange.
Propriétés:
Il a donc toutes les propriétés des rectangles et des losanges.