Cours de perspective 01.pmd

Cours de perspective de M. Beuriot
Leçon 1.
Construction des formes de base
Bref résumé appliqué à l’étude de la perspective.
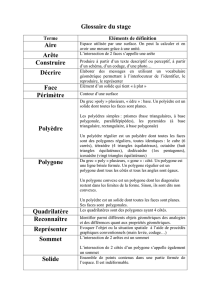
Il ne serait pas inutile de donner un bref résumé des noms et définitions des figures géométriques les plus
employées en perspective. Ce sera une leçon très brève, d’où nous exclurons les figures géométriques les plus
connues, comme « la ligne droite, verticale, horizontale », ou celles qui n’ont pas d’application pratique dans le
dessin en perspective comme « la droite sécante, le rayon ».
Segment : c’est un fragment de ligne droite, en partant du fait que, théoriquement, une ligne droite est définie.
Parallèles : Ce sont deux lignes droites, à égale distance l’une de l’autre, qui, même si on les prolonge, ne
peuvent ce rencontrer.
Lignes convergentes : ce sont deux ou plusieurs lignes limitées par un même point. En perspective, on dira
qu’elles fuient vers un même point.
Sommet : C’est le point où se réunissent deux ou plusieurs lignes convergentes. En perspective, on l’appelle
« le point de fuite ».
1
Polygone : c’est une figure géométrique plane.
Ligne polygonale ou brisée : c’est une figure quelconque, formée par plusieurs segments ou parties d’une ligne
droite.
Plan : C’est une surface plane ou un espace quelconque, représenté par un polygone.
Carré : C’est un polygone qui a quatre côtés égaux et parallèles deux à deux et quatre angles droits.
Rectangle : C’est un polygone qui à quatre côtés, égaux deux à deux, et qui à quatre angles droits.
Losange : C’est également un polygone, qui ,a quatre côtés égaux, mais qui n’a pas d’angle droit.
Cercle : C’est la surface ou l’espace contenu dans une circonférence.
2
Diamètre : C’est le segment –ligne droite-, qui passe par le centre du cercle et est limité par la circonférence.
L’arc : C’est une partie d’une circonférence.
La mesure des arcs : L’arc ou partie d’une circonférence se mesure par le système sexagésimal.
La mesure des arcs et par conséquent celle de la circonférence est l’un des points intéressant à rappeler, en ce
qui concerne l’étude de la perspective.
Tout commença il y a des milliers d’années par l’établissement du système de mesure sexagésimal. Vous savez
qu’il y a le système décimal fondé sur le chiffre dix et sur un compte de dix en dix. Mais dans la civilisation
chaldéo-assyrienne, les hommes inventèrent le système sexagésimal, fondé sur le nombre 60.
A cette époque, la roue était déjà inventée et ils appliquèrent leur système de mesure à la circonférence qu’ils
divisèrent en 360 parties (c’est à dire 60X6).
Chacune de ces 360 parties sera un degré ou une partie de la circonférence.
Chacun de ces degrés, nous le diviserons en 60 minutes.
Chacune de ces minutes sera divisée en 60 secondes (ne confondez pas une minute ou une seconde de temps
avec une minute ou une seconde de circonférence).
En somme la circonférence était divisée en degrés, minutes et secondes.
Pour traduire ces unités on utilise ces signes :
Degré °
Minute ’
Seconde»
Ainsi, une mesure de 30 degrés, 15 minutes et 40 secondes s’écrit :
30° 15’ 40»
3
Un angle: est une figure formée par deux lignes droites, partant d’un point commun. Pour mesurer l’ouverture
d’un angle, il faut considérer la mesure de son arc. Car en fait, un angle, n’est rien d’autre qu’une partie de
cercle.
Ici se ferme la parenthèse, et se poursuit le bref résumé de géométrie avec ses définitions visualisées.
Angle droit : C’est un angle ayant ses deux côtés perpendiculaires (A), et mesurant 90°, c’est à dire le quart de
la circonférence.
Perpendiculaire : la perpendiculaire est la droite qui forme un angle droit, avec une autre droite donnée. On dit
par exemple, soit une droite perpendiculaire à l’horizontale A, soit une droite perpendiculaire à la verticale B.
Oblique : C’est une ligne inclinée, qui forme un angle avec une droite.
4
L’angle aigu : C’est un angle plus petit qu’un angle droit. Sa mesure doit être inférieure à 90°.
L’angle obtus : C’est un angle plus grand qu’un angle droit, qui mesure donc plus de 90°.
Le triangle : C’est une figure formée par trois droites qui se coupent. Il y a diverses sortes de triangles, dont
deux sont illustrées ici : Le triangle équilatéral qui a ses trois côtés égaux, et le triangle rectangle , qui a un
angle droit.
Le polyèdre : C’est un corps quelconque limité par
plusieurs surfaces planes. C’est le nom générique de
tous les corps qui ont une surface plane : le cube, le
prisme ; la pyramide, le parallélépipède, etc.
Le parallélépipède : C’est un polyèdre à six faces égales deux à deux et parallèles. Comme tous les polyèdres,
il y a des faces, des sommets, et des arêtes. Le plus courant est le parallélépipède rectangle.
5
Le cube : C’est le plus important des polyèdres. Il comprend six faces qui sont toutes carrées.
Le prisme : C’est un polyèdre limité par deux polygones égaux, dont les faces latérales sont des
parallélogrammes (quadrilatère dont les côtés opposés sont parallèles).
La pyramide : C’est un polyèdre qui a pour base un polygone quelconque, et pour faces latérales, des triangles
qui se réunissent en un même point appelé sommet .
Le tronc : C’est une partie restante d’un pyramide ou d’un cône, sectionnée par un plan parallèle à la base.
6