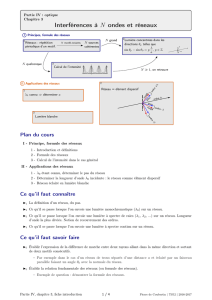
d p F Σ =

Bac S 2017 Liban Correction © http://labolycee.org
EXERCICE III : INTERFÉRENCES AVEC DES ATOMES FROIDS (5 points)
1. Chute de l’atome avec le modèle de Newton
1.1. Appliquons la 2
ème
loi de Newton au système {atome} dans le référentiel lié
au gravimètre, considéré galiléen pendant la durée de l’étude :
EXT
dp
F
dt
Σ = .
Comme la masse du système ne change pas, on a
EXT
F ma
Σ =
.
Le système étant en chute libre, il n’est soumis qu’à son poids
.
P mg
=
Donc . .
mg ma a g
= ⇔ =
On utilise un repère
(
)
O i j
, ,
où
O
est la position initiale du système.
Ainsi
0
x
y
a
a
a g
=
=
= −
Par définition
dv
a
dt
= ; en primitivant, on obtient :
1
2
x
y
v C
v
v g t C
=
= − +
.
or
0
00
0
0
x
y
v
vv
=
=
donc
0
x
y
v
v
v g t
=
= −
.
La composante de
v
sur l’axe des abscisses est nulle tandis que celle sur l’axe des ordonnées est non
nulle donc le vecteur vitesse est bien vertical.
Il reste maintenant à retrouver l’expression de v
F
proposée :
Au point F (au niveau de la double fente) :
0
x
F
y F
v
v
v g t
=
= −
.
Par définition
dOG
v
dt
= ; en primitivant, on obtient :
3
2
4
1
2
x C
OG
y g t C
=
= − +
. .
or
0
00
0
0
x
OG y
=
=
donc
2
01
2
x
OG
y g t
=
= −
. .
On en déduit qu’au point F,
2
1
2
F F
y g t
= −
. .
par ailleurs y
F
= – L
2
1
2
F
g t L
=
. . donc
2
.
F
L
t
g
=
En injectant cette expression dans celle de
v
:
2
0
2 2 2
x
Fy
v
vL Lg
v g Lg
g g
=
= − = − = −
. . .
. . .
Par définition,
2 2
0 2 2
. . . .
F F Fx Fy
v v v v Lg Lg
= = + = + =
Autre méthode : C’est aussi de la mécanique de Newton. Il est plus simple d’utiliser la conservation de
l’énergie mécanique lors d’une chute libre. On choisit comme référence E
PP
= 0 au point O.
( ) ( )
m m
E O E F
= donc
( ) ( ) ( ) ( )
c pp c pp
E O E O E F E F
+ = +
2
1
0 0 2
. . . .
F
mv mg L
+ = − donc 2
. .
F
v g L
=
O
j
i
double fente
L
F

1.2. Dans le cadre de la mécanique de Newton, chaque atome passe par une des deux fentes et donne
un impact sur l’écran correspondant à ce passage. La situation proposée ici ressemble plus à celle
représentée à droite ci-dessous.
D’après le site https://toutestquantique.fr/
Voir la vidéo : https://youtu.be/JlsPC2BW_UI
D’après la vidéo réalisée par le Synchroton Soleil
https://youtu.be/N968DgSVLkg?t=4m23s
2. Le modèle de de Broglie
2.1. Le phénomène d’interférences est caractéristique des ondes : cette expérience prouve le caractère
ondulatoire de la matière (onde de matière).
2.2. Par définition de la quantité de mouvement : p = m . v
F
1 1
kg.m.s kg m.s
− −
2.3. La relation de de Broglie relie l’aspect particulaire et l’aspect ondulatoire de la matière :
h
p
=
λ
Donc
.
th
F
h h
p mv
= = λ
34
26
6 63 10
3 35 10 12
th
−
−
×
= =
× ×
,
, ,
λ 1,6×10
–8
m comme indiqué.
2.4. L’interfrange est la plus distance entre deux franges de même nature. Pour plus de précision, on
mesure plusieurs interfranges. Soit de centre à centre de zones sombres (2i), soit de centre à centre de
zones claires (3i).
ou
2.5. Seule la relation
.
D
i
d
=
λ
est homogène : on en conclut que c’est elle qui convient.
Démonstration :
.
D
i
d
=
λ
donne
m.m
m m
m
⇔ ⇔ donc relation homogène
2
.
d
i
D
=
λ
donne
2
2
m .m
m m
m
⇔ ⇔ donc relation non homogène
2
.
d D
i=
λ
donne
2
m.m
m sans unité
m
⇔ ⇔ donc relation non homogène
3 2 4 cm 1 2 4
0 22 mm
1 mm 3,6 cm 3 6 3
,,,
,
ii ⇔×
= =
⇔×
i
i
i
i
i
2 16 cm 1 16
0 22 mm
1 mm 3,6 cm 3 6 2
ii ⇔×
= =
⇔×
,,,
,

2.6. On en déduit
exp
.
i d
D
= λ alors
3 6 8 8
3
0 22 10 6 10
12 10 m 1 10 m
113 10
exp
,,
− − − −
−
× × ×
= = × ≈ ×
×
λ (1
CS en toute rigueur)
2.7. On constate donc que
exp
λ
<
th
λ
(
8
12 10 m
,
−
× <
8
16 10 m
,
−
× ).
2.8.1. Vu que la gravitation continue de s’exercer sur les atomes, alors leur vitesse continue d’augmenter
après les fentes et donc leur quantité de mouvement p = m . v augmente également.
2.8.2. Vu que
p
augmente, la longueur d’onde de matière donnée par la relation de de Broglie diminue
car
h
p
=
λ avec h = Cte.
2.8.3. On aurait donc dû comparer
exp
.
i d
D
= λ qui correspond aux interférences des ondes de matière sur
l’écran avec la longueur d’onde de matière qui arrive sur l’écran et pas sur les fentes.
NON DEMANDÉ :
Par analogie, on applique la relation 2
. .
F
v Lg
= pour la chute libre jusqu’à l’écran : 2
.( ).
E
v L D g
= +
La longueur d’onde de de Broglie de l’onde de matière qui arrive sur l’écran est :
2
.
. .( ).
E
h h h
p mv
m L D g
= = = + λ
AN :
34 8
26 3
6 63 10
10 10 m
3 35 10 2 76 113 10 9 8
,,
, ( ) ,
−−
− −
×
= = ×
× × × + × ×
λ
Ce résultat est plus proche du résultat expérimental que le résultat précédent.
Compétences exigibles ou attendues :
En noir : officiel (Au B.O.)
En italique : officieux (au regard des sujets de bac depuis 2013)
□ Extraire et exploiter des informations sur les ondes de matière et sur la dualité onde-particule.
□ Choisir un référentiel d’étude.
□ Connaître et exploiter les trois lois de Newton ; les mettre en œuvre pour étudier des mouvements
dans des champs de pesanteur et électrostatique uniformes.
□ Exploiter les équations horaires du mouvement ou l’équation de la trajectoire pour répondre à un
problème donné (ex : portée d’un tir, durée d’une chute, vitesse en un point …).
□ Savoir que le phénomène d’interférences est caractéristique des ondes.
□ Définir la quantité de mouvement d’un point matériel.
□ Connaître et utiliser la relation de de Broglie :
h
p
=
λ