chapitre18_bissectrice_et_cercle_inscrit.docx

A
B C
M
H
F
A
B C
M
H
F
D
Chapitre 18
BISSECTRICE ET CERCLE INSCRIT
L’ensemble des points situés à égale distance des
côtés d’un angle est la bissectrice de cet angle.
Démonstration :
Sens direct
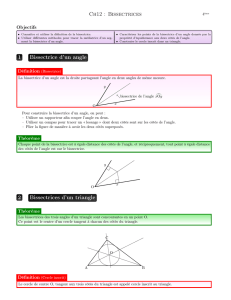
Montrons d’abord que si un point est équidistant des côtés
d’un angle alors il appartient à la bissectrice de cet angle.
Soit ;BCA un angle.
Soit M un point situé à égale distance des côtés de l’angle.
Soient F et H les points appartenant respectivement à [CA)
et [CB) tels que : (MF) (CA)
(MH) (CB)
Donc MF = MH.
Comme MFC et MHC sont des triangles rectangles en F et H alors :
Error!
=
Error!
donc cos ;CMF = cos ;CMH
donc ;CMF = ;CMH
On en déduit que ;FCM et ;HCM ont la même mesure.
Donc M appartient à la bissectrice de ;ABC.
Réciproque
Soient l’angle ;BCA, M un point de la bissectrice de ;BCA et les points F et H définis ci-dessus.
Donc ;FCM et ;HCM ont la même mesure.
Donc ;CMF et ;CMH aussi.
Donc : cos ;CMF = cos ;CMH.
Donc :
Error!
=
Error!
d’où MF = MH. ■
Propriété : Les trois bissectrices des angles d’un triangle sont concourantes en un
point I, appelé le centre du cercle inscrit de ce triangle.
Démonstration :
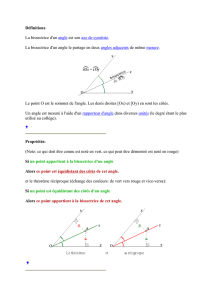
Soit un triangle ABC.
Soit M un point appartenant à la
bissectrice de ;BAC et à celle de
;ABC.
Soient D, F et H les points respectifs de
[AB], [AC] et [BC] tels que :

(MD) (AB)
(MF) (CA)
(MH) (BC)
M est un point équidistant des côtés de ;BAC et des côtés de ;ABC.
Donc : MD = MF
MD = MH
Donc : MF = MH.
D’où M est également un point de la bissectrice de ;BCA.
Les trois bissectrices sont donc bien concourantes.
Appelons (C) le cercle de centre M et de rayon MD.
Comme : (MD) (AB)
(MF) (CA)
et (MH) (BC)
donc (AB), (AC) et (BC) sont tangentes à (C) respectivement en D, F et H.
Donc le cercle (C) est inscrit dans le triangle ABC. ■