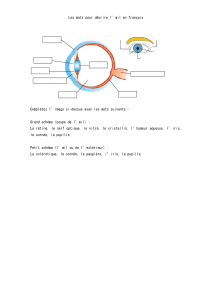
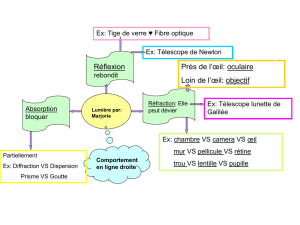
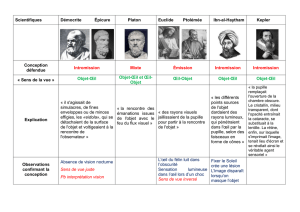
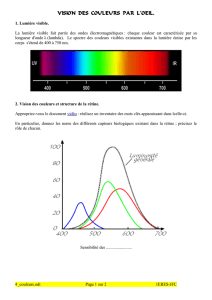
limites d`un instrument astronomique - Erquy-nox

Erquy-Nox
LIMITES D’UN INSTRUMENT ASTRONOMIQUE
© Erquy-Nox avril 2013
1
A partir des caractéristiques d’un instrument on peut faire un certain nombre de calculs qui donneront des
indications sur les limites et donc sur les performances d’un instrument.
Le grossissement maximum d’un instrument :
C’est le grossissement maximum théorique d’un instrument pour lequel l’image reste nette. Il correspond à 2 fois le
Ø de l’instrument.
 Gmax = 2xD
Ex pour un T200/1000 Gmax = 2x200 = 400, on peut théoriquement grossir jusqu’à 400 fois.
Dans la pratique, le grossissement max est lié à la qualité de l’instrument, et aux conditions d’observation
(turbulence, transparence…). En fait avec un instrument de qualité on peut grossir au-delà de Gmax, l’image sera
juste plus sombre, et semblera un peu floue.
Le grossissement résolvant d’un instrument :
C’est le grossissement théorique à partir duquel tous les détails de l’image sont visibles. Grossir au-delà donnera une
image certes plus grosse mais pas de détails supplémentaires visibles. Il dépend de la qualité de l’œil de
l’observateur à percevoir les détails.
 Si le pouvoir de résolution de l’œil est 1’ (œil performant) alors Gres = D/2
 Si le pouvoir de résolution de l’œil est 2’ (œil moins performant) alors Gres = D
Ex pour un T200/1000
 Un observateur ayant un œil performant aura besoin de grossir 200/2 = 100 fois pour voir tous les détails.
 Un observateur ayant un œil moins performant aura besoin de grossir 200 fois pour voir tous les détails.
Le grossissement équipupillaire d’un instrument :
C’est le grossissement pour lequel la pupille de sortie sera égale à la pupille de sortie de l’observateur. Ce calcul
permet de choisir le meilleur oculaire par rapport à la pupille de sortie max de l’observateur.
Gequi = D/pupille max
Ex pour un T200/1000
 Pour un observateur ayant une Ps = 6, le Gequi = 200/6 = 33, l’observateur optera pour un oculaire qui
grossira 33 fois.
 Pour un observateur ayant une Ps = 5, le Gequi = 200/5 = 40, l’observateur optera pour un oculaire qui
grossira 40 fois.

Erquy-Nox
LIMITES D’UN INSTRUMENT ASTRONOMIQUE
© Erquy-Nox avril 2013
2
La magnitude limite d’un instrument :
La magnitude théorique limite dépend du Ø de l’instrument, elle est donné par la formule : Mth = 2.1 + 5logD
Ex pour un T200/1000
 Mth = 2.1 + 5logD = 2.1 +5log200 = 13.6
En pratique la magnitude limite de l’instrument va dépendre de la qualité du ciel, donc de la pollution lumineuse et
de la magnitude que l’œil de l’observateur peut atteindre. La magnitude limite de l’instrument est alors donnée par
la formule : M = moeil + 5log(D/6) où 6 est la magnitude limite de que l’observateur peut atteindre (pupille dilaté à 6
mm).
L’échelle de Bortle : elle a été définie en 2001 par John Bortle dans le magazine Sky and Telescop.
Classe
Code couleur
Type de ciel
Plus petite magnitude visible
1
Noir
Excellent ciel noir
7.6 - 8
2
Gris
Ciel noir typique
7.1 - 7.5
3
Bleu
Ciel rural
6.6 - 7
4
Vert
Jaune
Transition rural / périurbain
6.1 - 6.5
5
Orange
Ciel de banlieue
5.6 - 6
6
Rouge
Ciel de banlieue éclairée
5.1 - 5.5
7
Rouge
Transition banlieue / ville
4.6 - 5
8
Blanc
Ciel urbain
4.1 - 4.5
9
Blanc
Ciel de centre ville
4 au mieux
Ex pour T200/1000
 Dans le cas d’une pollution lumineuse à 9 M = moeil + 5log(D/6) = 4 + 5log(200/6) = 11.6
 Dans le cas d’une pollution lumineuse à 1 M = moeil + 5log(D/6) = 8 + 5log(200/6) = 15.6
La clarté d’un instrument :
C’est la quantité de lumière collectée par l’instrument par rapport à celle que collecte l’œil avec une pupille de 6mm.
La clarté est définie par la formule : Clarté = D2/62
Ex pour un T200/1000
 Clarté = D2/62 = 2002/62 = 40 000/36 = 1 111, donc un T200 collecte 1 111 fois plus de lumière que l’œil.
Le pouvoir séparateur d’un instrument :
C’est la faculté de l’instrument à résoudre les objets, c'est-à-dire la distance minimale qu’il faut entre 2 points
(étoiles) pour que le télescope arrive à les résoudre. Cette distance dépend du Ø, et est exprimée en seconde d’arc.
Le pouvoir séparateur se calcul grâce à la formule : Pouvoir séparateur S = 120/D
 Ex pour un T200 le pouvoir séparateur S = 120/D = 120/200 = 0.6’’
 Ex pour un T114 le pouvoir séparateur S = 120/D = 120/114 = 1.05’’

Erquy-Nox
LIMITES D’UN INSTRUMENT ASTRONOMIQUE
© Erquy-Nox avril 2013
3
120/D : forme cacahuète 280/D : deux disques tangents les étoiles sont individualisées
Résolution d’un instrument :
C’est la taille minimale des détails que l’on peut observer sur un objet. Elle dépend du pouvoir séparateur et de la
distance de l’objet. Résolution R = L.tan 
 (où L est la distance à laquelle se situe l’objet observé).
Ex pour T200/1000
 Lune (384 000 km), R = 384 000 .tan 
 = 1.1 km, le plus petit détail visible sur la Lune sera de 1.1 km
Conclusion : tous les calculs sur les limites théoriques d’un instrument font intervenir le Ø, et donc sans surprise plus
celui-ci est important meilleures sont les performances de l’instrument.
Cependant il ne faut pas oublier que tous les calculs sont théoriques, ils sont valables pour des conditions
d’observation excellentes, pour un instrument bien réglé (par ex la collimation pour le pouvoir de séparation), et
pour un observateur ayant une bonne vision.
Quelques exemples :
Ø de l’instrument en mm
Gmax
Gres (1’)
Gequi
Mth
M à 4
Clarté
S
R
L70
100
35
12
11.3
9.3
136
1.7
3.16
L80
160
40
13
11.6
9.6
178
1.5
2.79
T114
228
57
19
12.4
10.4
361
1
1.86
T200
400
100
33
13.6
11.6
1 111
0.6
1.18
T250
500
125
42
14
12
1 736
0.48
0.89
T300
600
150
50
14.5
12.5
2 500
0.4
0.74