20_05_complexes_correction.pdf (35.52 KB)

TS3 Révisions du 20/05 (thème : nombres complexes) Année 2010/2011
EXERCICE 1
1. On a p2
2(−1+i) =−p2 2+ip2 2=cos 3π 4+isin 3π 4=e3π
4, donc fa pour écriture complexe z′=e3π 4z.
La transformation fest donc la rotation de centre O et d’angle 3π
4.
2. (a) Pour tout entier naturek n, notons Pnla proposition : "‘zn=ei¡3nπ
4¢"’ Montrons, par récurrence sur n, que
la proposition est vraie pour tout entier naturel n:
•Initialisation : z0=1=ei¡3×0π
4¢:P0est vraie.
•Supposons qu’il existe un naturel ktel que Pksoit vraie, c’est-à-dire : zk=ei³3kπ
4´.
Alors zk+1=ei3π
4×ei³3kπ
4´=ei³3(k+1)π 4´:Pk+1est vraie. La propriété est héréditaire.
Conclusion : on a démontré par récurrence que quel que soit n∈N,
zn=ei¡3nπ
4¢.
(b) Voir la figure plus bas.
(c) Mna pour affixe zndont un argument est 3nπ
4;
Mn+8a pour affixe zn+8dont un argument est 3(n+8)π
4.
Or 3(n+8)π
4=(3n+24)π 4=3nπ 4+24π 4=3nπ 4+6π.
On a donc arg(zn)=arg(zn+8)[2π]
Comme znet zn+8ont le même module et un même argument, les points Mnet Mn+8sont confondus.
3. Par la rotation f, le triangle M7M0M1a pour image le triangle M8M1M2, soit d’après la question précédente
(puisque M8=M0) le triangle M0M1M2.
Comme la rotation est une isométrie, elle conserve les longueurs, donc les aires : les triangles M0M1M2et
M7M0M1ont la même aire.
Le point M1a pour coordonnées Ã−p2
2;p2 2!.
On a donc M1M7=p2 et la hauteur du triangle M7M0M1issue de M0a pour longueur 1 +p2
2.
L’aire de ce triangle est donc égale à :
p2×Ã1+p2
2!
2=1+p2 2.
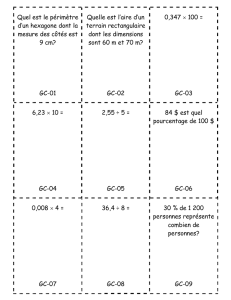
−1
−1−→
u
−→
v
OM0
M1
M2
M3
M4
M7
Page 1/2

TS3 Révisions du 20/05 (thème : nombres complexes) Année 2010/2011
EXERCICE 2
1. (a) On a I(0 ; 1) et A³p3 ; 2´; donc IA2=³p3´2+(2 −1)2=3+1=4=22⇒IA =2.
Le point A appartient au cercle Γde centre le point I et de rayon 2 Pour construire le point A, il suffit de
tracer la droite d’équation y=2, contenant le point (0 ; 2), qui coupe le cercle Γde centre I, de rayon 2. A
est le point d’abscisse positive.
(b) Par définition un point Md’affixe za pour image M′d’affixe z′tel que z′−zI=eiπ
2(z−zI)soit z−i=
i(z−i) ⇐⇒ z=iz+1+i.
Donc zB=i³p3+2i´+1+i=ip3−2+1+i=−1+i³p3+1´.
La rotation est une isométrie, donc IA = IB = 2, d’après la question 1. a. Le point B appartient donc au cercle
Γ.
(c) Par définition du milieu xI=xA+xC
2soit 0 =p3+xC 2⇐⇒ xC=−p3.
De même yI=yA+yC
2soit 1 =2+yC 2⇐⇒ yC=0.
Conclusion zC=−p3.
Remarque : on aurait pu dire que C est l’image de B par la rotation r
(d) Par définition de la rotation (BI) est perpendiculaire à (IA). D’autre part [AC] est un diamètre de Γ.
Le triangle ABC est inscrit dans le cercle Γdont un de ses côtés est un diamètre ; il est donc rectangle en B
et (BI) étant à la fois hauteur et médiane, le triangle ABC est isocèle en B.
Le triangle ABC est rectangle isocèle en B.
2. Il semble que (BF) et (CE) sont perpendiculaires.
Démonstration :
De −→ AE =−→ IB et −→ FA =−→ IB , on déduit que −→ FA =−→ AE , c’est-à-dire que A est le milieu de [EF].
D’autre part BI = IA = 2 = EA = AF : donc le triangle EIF est inscrit dans le cercle de diamètre [EF] : il est donc
rectangle en I.
De plus (BI) ⊥(AC) et −→ AE =−→ IB entraîne que (AE) et (IB) sont parallèles, donc (AC) est perpendiculaire à (AE).
Dans le triangle EIF la droite (IA) est à la fois hauteur et médiane : ce triangle est donc rectangle isocèle en I.
Par la rotation r:
- B a pour image C
- F a pour image E
Par définition de rrotation d’angle π
2, la droite (BF) a pour image la droite perpendiculaire (CE).
−4
−4
++
+
+
+
+
O
I
A
B
2
E
F
C
−→
u
−→
v
Page 2/2