15 Prisme droit et cylindre de révolution

Maths 5e15. Prisme droit et cylindre de révolution 2012-2013
15 Prisme droit et cylindre de révolution
15.1 Dessin en perspective (rappel)
Règles du dessin en perspective cavalière :
1
!Les arêtes de l’objet qui sont parallèles, sont représentés par des segments parallèles.
2
!Ce qui est vu de face est représenté en vraie grandeur (ou à l’échelle) et les angles
sont conservés.
3
!Les arêtes fuyantes sont représentées avec une échelle plus petite que celle de la vue
de face (par exemple la moitié) ;
les mesures des angles des faces fuyantes ne sont pas conservées.
Exemples :cubeetempilementsdecinqcubes
Remarque :Lesarêtescachéespeuventêtrereprésentéesentraitinterrompu pour la
compréhension du dessin.
15.2 Prisme droit
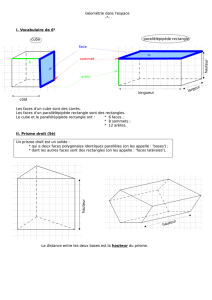
Définition :Unprismedroitestunsolideconstituédedeux faces parallèles identiques
reliées entre-elles par des rectangles.Lesdeuxfacesparallèless’appellentlesbases et les
faces rectangulaires qui les relient s’appellent les faces latérales.Ladistanceentreles
deux bases s’appelle la hauteur :c’estaussilalongueurcommuneàdeuxfaceslatérales
contiguës.
bases hexagonales bases triangulaires bases rectangulaires
Remarque :Lepavédroitestunprismedroitparticulierdontlesbasessont des rectangles ;
F.Bonomi – 34/36 – prog 2006

Maths 5e15. Prisme droit et cylindre de révolution 2012-2013
deux faces opposées quelconques du pavé droit sont des bases de ce prisme droit.
Remarques :Unprismedroitdontlesbasessontdespolygonesàncôtés il y a :
•nfaces latérales, soit n+2facesautotal(encomptantles2bases);
•3narêtes (ncôtés pour chacune des deux bases et narêtes reliant chacun des nsommets
d’une base à son homologue de l’autre base) ;
•2nsommets (nsommets pour chacune des deux bases).
15.3 Patron d’un prisme droit
Patron :Lepatrond’unsolideestunefigureplaneconstituéedetoutes les faces du solide
assemblées entre-elles par des arêtes.
Exemples :OncoupelepavédroitABCDEF GH suivant un plan passant par les dia-
gonales de face [AC]et[EG]:onobtientainsideuxprismesdroitsàbasestriangulaires
identiques (ABCEF G et ADCEHG)dontunpatronestdessinéci-dessous.
AB
C
D
EF
G
H
AB
FE
CC
C
GG
G
15.4 Cylindre de révolution
Définition :Uncylindrederévolutionestunsolideconstituédedeuxdisques parallèles,
appelés bases,reliésentre-euxparunrectangleconstituantlaface latérale du cylindre.
La distance entre les deux bases s’appelle la hauteur.
Exemples :Lesfiguresci-dessousmontrentdeuxdessinsenperspectivecavalièresde
cylindres de révolution.
15.5 Patron d’un cylindre de révolution
Le patron d’un cylindre de révolution est constitué des deux disques de base et d’un
rectangle dont la longueur de l’un des côtés est la hauteur du cylindre de révolution et
la longueur de l’autre est égale au périmètre du disque de base.
F.Bonomi – 35/36 – prog 2006

Maths 5e15. Prisme droit et cylindre de révolution 2012-2013
15.6 Volume du prisme droit et du cylindre de révolution
Le volume d’un prisme droit ou d’un cylindre de révolution estV=B×h,
où Best l’aire de la base et hla hauteur du solide.
7m
4m
7m
12 m
Exemple :Unemaisonàlaformed’unprisme
(voir schéma). Calculer le volume de cette mai-
son.
Solution :Labaseestunpentagonepouvantêtredé-
composé en un rectangle de 7 m sur 4 m et un triangle
isocèle de base 7 m et de hauteur 3 m par rapport à
cette base. Son aire est donc B=4×7+ 7×3
2=
38,5m
2.
alors le volume du prisme droit est V=38,5×12 = 462 m3.!
Dans le cas d’un cylindre de révolution la base est un disque. L’aire d’un disque de rayon
rest B=πr2,oùπ≈3,141592653589 ...≈3,14
(utiliser la touche πde la calculatrice).
Exemple :Unrouleaudepapieressuie-toutestuncylindrede11cmdediamètre percé
d’un trou de 36 mm de diamètre en son centre et de hauteur 23,5 cm. Calculer le volume
de papier.
Solution :L’airededisquedebaseestdeB=π×5,52−π×1,82=π(5,52−1,82)≈84,85 cm2;
volume de papier V=84,85 ×23,5≈1994cm
2(arrondi à l’unité).
15.7 Aire du prisme droit et du cylindre de révolution
L’aire d’un solide est la somme des aires de toutes les faces decesolide.
Pour un prisme droit ou un cylindre de révolution c’est la somme des aires des deux bases
et de l’aire latérale (somme des aires des faces latérales).
Aire latérale : A=p×h,oùpest le périmètre d’une base et hla hauteur de ce solide.
Exemple :L’aired’uncylindrederévolutionde10cmdediamètreetdehauteur 40 cm,
vaut : A=2×π52+10π×40 = 450π≈1414 cm2
F.Bonomi – 36/36 – prog 2006