e1 14-15_cor

1|4
Epreuve de Physique
Nom:
No:
SérieE1;février2015
Classe:3eme
Durée:55minutes
L’usage de la calculatrice scientifique est autorisé.
Les figures de l’exercice 1 et exercice 2 seront travaillées sur la fiche annexe de la page 4.
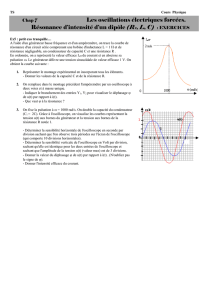
Exercice 1 : Image donnée par une lentille convergente (7 points)
Le schéma ci-dessous montre :
une lentille (L) convergente, son axe optique et ses deux foyers objet et image F et F’. la distance
focale étant de 3 cm.
I- On donne :
- l’image A’B’, de l’objet AB, donnée par (L) ;
- un rayon particulier, issu de B, dont la direction passe par F et qui rencontre la lentille en I.
- le rayon émergent KF’ d’un rayon incident particulier issu de B.
1. Tracer, avec justification, sur la figure- voir annexe.
a. le trajet du rayon émergent correspondant au rayon incident FI.
Le rayon émerge de la lentille parallèlement a son axe optique puisque le rayon incident
provient de son foyer objet F
b. le rayon incident correspondant au rayon émergent KF’.
Le rayon incident LK est parallèle à l’axe optique de la lentille (L). ce rayon atteint la lentille
au point K.
2. a. Construire alors l’objet AB.
B est le point d’intersection des deux rayons incidents LK et FI.
b. Déterminer graphiquement :
i. la grandeur de l’objet AB. AB= 1 x 1 = 1 cm.
ii. la position de l’objet AB par rapport à la lentille. AO= 2 x 1 = 2 cm.
3. a. Quelle est la nature de A’B’? A’B’ est une image virtuelle.
b. Déterminer graphiquement la grandeur de l’image et sa position par rapport à la lentille.
A’B’ = 3x 1 = 3 cm

2|4
4. En comparant les caractéristiques de l’image à celles de l’objet, déduire que la lentille (L) joue,
dans ce cas, le rôle d’une loupe.
La lentille donne de l’objet une image droite et plus grande ce qui correspond a une loupe.
II- On place maintenant l’objet à 6 cm de la lentille (L) convergente.
a. Sans faire un schéma, donner la nature de l’image A’B’ et son orientation.
A’B’ est une image réelle puisque l’objet est placé a une distance supérieure a la distance focale.
b. Déterminer la distance séparant A’B’ de la lentille (L).
A’O= OA = 2f onc A’O = 6cm
c. Comparer sa taille à celle de l’objet.
A’B’ = AB= 1 cm
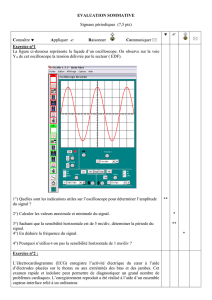
Exercice 2 : Etude d’une tension à l’aide d’un oscilloscope (7 points)
I- Une lampe (L), portant l’indication « 12 V », est branchée sur les bornes d’un GBF, délivrant une
tension variable ; la lampe brille normalement.
On branche entre les bornes du générateur un oscilloscope. On observe l’oscillogramme ci-dessous.
La sensibilité horizontale est : 5 ms/div.
1. Faire le schéma du montage réalisé montrant ainsi le générateur ,la lampe et l’oscilloscope.
2. Donner la signification de l’indication « 12V » de la lampe.
L’indication « 12 V », représente la tension nominale efficace de la lampe. C’est la tension
efficace sous laquelle la lampe brille normalement.
3. a. Quelle est la valeur efficace de la tension délivrée par le générateur ? Justifier.
Puisque la lampe brille normalement, donc la tension efficace du générateur est « 12 V ».
1) b. En déduire la valeur maximale de la tension du GBF (arrondir la réponse à l’unité).
La tension du générateur est sinusoïdale, donc sa valeur maximale est :
 2122UUm 17 V.
4. L’oscillogramme de la tension du G.B.F. est donné dans la figure ci-contre.
En l’absence de la tension, la ligne lumineuse horizontale passe par le centre de l’écran de
l’oscilloscope.

3|4
D
I
CB
A
P
G
R
1
R
2
N
R
3F
I2
I1
a. Quelle est la nature de la tension delivrée par le générateur ?
La tension est alternative sinusoidale.
b. Calculer la sensibilité verticale de l’oscilloscope.
On a Um = 17 V, et d’après l’oscillogramme de l’oscilloscope, on peut tirer : ym = 3,4 div
La sensibilité verticale est : div 3,4
V 17
y
U
S
m
m
V = 5 V/div.
c. Calculer la période et la fréquence de cette tension.
T = Sh x = 5 x 4 = 20 ms
La fréquence de la tension est : f= 1/T = 1/ (0,02) = 50 Hz
II- On alimente la lampe (L) avec un générateur de tension continue UPN.
(L) fonctionne normalement sous cette tension.
1. Quelle doit être la valeur UPN de la tension délivrée par le générateur ?
UPN = 12 V ( valeur efficace)
2. On branche entre les bornes du générateur un oscilloscope. L’entrée de l’oscilloscope est
connectée à la borne N du générateur. La sensibilité verticale est : Sv = 5V/div.
a. L’oscilloscope visualise-t-il UPN ou UNP ? Justifier.
UNP
b. Faire un schéma représentant le branchement du générateur à l’oscilloscope.
c. Représenter sur la figure-voir annexe, l’oscillogramme de cette tension. Justifier.
3. Que se passe-t-il à l’oscillogramme lorsqu’on :
a. inverse les branchements de l’oscilloscope sur la pile ?
La trace se décale de 2,4 divisions vers le haut a partir de l’axe médian.
b. change la sensibilité verticale à la valeur SV = 10V/div?
La trace se décale de 1,2 divisions a partir de l’axe médian.
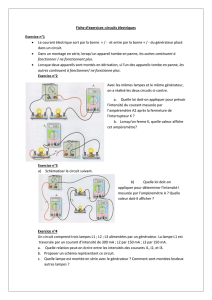
Exercice 3 : Etude d’un circuit électrique (6 points)
On réalise le montage de la figure suivante formé :
- d’un générateur de tension continue UPN
- de trois conducteurs ohmiques (R1), (R2) et (R3) de
résistances R1= R2 =100 Ω, R3 = 300 Ω.
On donne UAC= 6 V.

4|4
1. a. Quelle est la valeur de la tension UCB.
UCB = UAC = 6 V les deux conducteurs R1 et R2 étant identiques.
b. Déduire la valeur de la tension UAB , UDF UPN.
UAB = UAC + UCB = 12 V
UDF = UAB = UPN = 12V
2. a. Calculer la valeur de la résistance équivalente à l’ensemble des trois conducteurs ohmiques
ainsi branchés.
R = R1 + R2 = 200 Ω
1/R + 1/ R3 = 1/200 + 1/ 300 =5/ 600 Req= 600/5 = 120 Ω
b. Déduire l’intensité I du courant débité par le générateur.
I = UPN / Req = 12/ 120 = 0,1 A
3. a. Déterminer les intensités I1 et I2 des courants.
I1 = UAC / R1 = 6/ 100 = 0, 06 A
I2 = UDF / R3 = 12/ 300 = 0, 04 A
b. Vérifier la loi d’additivité des intensités au point D.
I1 + I2 = 0,06 + 0,04 =0, 1 A et I =0, 1 A alors I= I1 + I2
4. a. Déterminer les puissances consommées par (R1), (R2) et (R3).
P1 = UAC x I1 = 6 x 0,06 = 0,36 W
P2 = P1= 0,36 W
P3 = UDF x I2 = 12x 0,04 = 0,48 W
b. Déduire la puissance totale consommée par le circuit.
P totale = P1 + P2 + P3 = 1,2 W
5. Déterminer en joules et en kWh l’énergie consommée par le circuit en 5 heures.
E = P x t = 1,2 x 5 x 3600 = 21 600 J
E= P x t = 0,0012 x 5 = 6 x 10-3 kWh.

5|4
Nom:
No:
Classe:
Fiche annexe à rendre avec la copie
Exercice 1 :
Exercice 2 :