Cinématique Etude d`un système de propulsion par hélice à pas

INSA de Lyon Lundi 26 Janvier 2009
2ème année
1
Cinématique
DS
Etude d’un système de propulsion par hélice à
pas variable
Présentation (D’après concours ESIM 2003)
La photographie ci-contre présente un remorqueur
équipé d'un système de propulsion (VSP : "Voith
Schneider Propeller") par hélice à pales
oscillantes. Ce système est une alternative à la
propulsion classique par hélice en bout d'arbre et
il offre de nombreux avantages en terme de
manœuvre (réactivité, sécurité et poussée
omnidirectionnelle). En particulier, il permet de
faire varier rapidement avec précision et en
continu la force de poussée d'un propulseur en
direction et intensité, élément déterminant pour
les navires devant être manœuvrés avec précision
dans un rayon limité.
Les navires sont toujours équipés de deux VSP
disposés longitudinalement ou frontalement (cas
étudié et présenté ci-contre). Pour tous les
schémas à venir (bateau et/ou propulseur seul), la
poupe (arrière) sera située à gauche, alors que la
proue (avant) se trouvera à droite.
Les deux propulseurs sont commandés
indépendamment. Une multitude de
configurations de commande peuvent être
envisagées et le tableau ci-dessous en montre
quelques-unes.
Neutre Avant toute Arrière toute Tribord toute

INSA de Lyon Lundi 26 Janvier 2009
2ème année
2
Le mécanisme permettant l’orientation des pales est présenté document 1. Il est constitué de
deux parties :
- Partie commande : la consigne d’orientation est définie par deux vérins qui imposent la
position du point C
- Partie orientation : le mouvement de propulsion est obtenu par la rotation, autour de
l’axe ),(
3,00
zO
r
, des ensembles articulés {2,3,4,5} qui supportent chaque pale 6.
L’orientation de chaque pale évolue au cours de la rotation et la configuration souhaitée
(neutre, avant toute, tribord toute, etc…) est obtenue en modifiant la position du point E
reliée à celle du point C par la tige 7.
Pour l’ensemble de l’étude la vitesse de déplacement du navire par rapport à l’eau est
négligée. Le bâti S
0
qui supporte le propulseur sera donc considéré comme immobile par
rapport à l’eau. Toutes les parties sont indépendantes.
1 – Etude du mécanisme d’orientation.
Ce mécanisme plan, schématisé document 2, assure une variation continue de l’incidence
des pales par rapport à l'écoulement. L’évolution de cette variation d’incidence est pilotée en
amplitude et direction par la position du point E. Ce point, localisé par ses coordonnées
polaires (
ce
ρρ −= et
ce
θθ =), est fixe par rapport au bâti 0 et le repère Rr qui permet de le
localiser servira de référence pour définir l’orientation de tous les solides en mouvement.
Le mécanisme est constitué des solides :
- 2 en liaison pivot d’axe ),(
2,0
zE
r
avec 0 Paramètre de mouvement : ),(
22
xx
r
r
r
= ϕ
- 3 en liaison pivot d’axe ),(
3,00
zO
r
avec 0 Paramètre de mouvement : ),(
3
xx
r
r
r
= β
- 4 en liaison pivot d’axe ),(
4,3,0
zF
r
avec 3 Paramètre de mouvement : ),(
44
xx
r
r
r
= ϕ
- 5 en liaison pivot d’axe ),(
5,2,0
zK
r
avec 2 Paramètre de mouvement : ),(
55
xx
r
r
r
= ϕ
- 6 en liaison pivot d’axe ),(
6,5,0
zL
r
avec 5 Paramètre de mouvement : ),(
66
xx
r
r
r
= ϕ
Par ailleurs :
- les solides 3 et 6 sont en liaison pivot d’axe ),(
6,3,0
zP
r
- les solides 2 et 4 sont en liaison pivot d’axe ),(
4,2,0
zH
r
1.1 – Ecrire les équations de liaison résultant des fermetures de chaînes en H et P.
1.2 - Donner la mobilité du système et préciser quel est (sont) le (ou les) paramètre(s) de
commande et les paramètres internes.
1.3 – Calculer la vitesse et l’accélération des points K et L dans leur mouvement par rapport à 0.
1.4 – Donner le torseur distributeur des vitesses du mouvement 6/0 en P et préciser la nature du
mouvement linéaire tangent.
1.5 – A partir de )(
0
3
PV
r
tracer sur le document 2 )(
0
3
FV
r
, )(
0
4
HV
r
, )(
0
5
KV
r
, )(
0
6
LV
r
ainsi que
les CIR (Centres Instantanés de Rotation) des mouvements 6/0 et 5/0.
Remarque : pour construire )()(
0
5
0
6
LVLV
r
r
= on utilisera l’équi-projectivité sur les
mouvements 6/0 et 5/0.
1.6 – Donner, en fonction des paramètres, la relation angulaire permettant de calculer
l’incidence de la pale par rapport à l’écoulement.

INSA de Lyon Lundi 26 Janvier 2009
2ème année
3
2 – Etude du mécanisme de commande.
Pour une configuration de commande donnée (avant toute, neutre, tribord toute, etc…) ce
mécanisme est immobile. Nous allons étudier sont fonctionnement lors du passage d’une
consigne de commande à une autre, c’est à dire lorsque l’on déplace le point C à l’aide des
vérins 1 et 2.
La présence de la pièce 7 (document 1) impose au point C de rester sur une sphère de centre
O . Les déplacements du point C étant de faible amplitude par rapport au rayon de cette
sphère, nous allons supposer que ce point reste dans le plan ),,(
00
*
yxO
r
r
et que le mécanisme
de commande peut être représenté par le schéma cinématique plan du document 3.
Le vérin 1 est constitué des pièces 10 et 11 :
- la pièce 10 est en liaison pivot d’axe ),(
10,0
zA
r
avec le bâti 0
paramètre de mouvement de 10/0 :
1
ψ
- la pièce 11 est en liaison glissière d’axe ),(
1
yA
r
avec la pièce 10
paramètre de mouvement de 11/10 :
1
. yAC r
→
= δ
Le vérin 2 est constitué des pièces 20 et 21 :
- la pièce 20 est en liaison pivot d’axe ),(
20,0
zB
r
avec le bâti 0
paramètre de mouvement de 20/0 :
2
ψ
- la pièce 21 est en liaison glissière d’axe ),(
2
xB
r
avec la pièce 20
paramètre de mouvement de 21/20 :
2
. xBC r
→
= µ
Par ailleurs les pièces 11 et 21 sont en liaison pivot de centre C.
2.1 – Ecrire les équations de liaison résultant de la fermeture de chaîne en C et définir la
mobilité du système.
2.2 – Relier les coordonnées polaires du point C (
c
ρ tel que
rc
xCO r ρ =
→
*
) et ),(
0rc
xx
r
r
= θ ) aux
paramètres de mouvement ),,,(
21
ψψµδ .
Remarque : On utilisera les deux chaînes fermées permettant de définir la positon du point C
à partir de la position du vérin 1 et de la position du vérin 2.
2.3 – En éliminant des équations précédentes les paramètres d’orientation des vérins ),(
21
ψψ ,
donner les deux équations permettant d’obtenir les coordonnées polaires du point C à partir
des paramètres de commande ),(
µ
δ
.
Remarque : on ne cherchera pas à résoudre ces équations.
2.4 – En vous appuyant sur la composition des vitesses en C dans les mouvements 11/0 =
11/10 + 10/0 et 21/0 = 21/20 + 20/0 tracer sur le document 3 les vitesses )(
0
10
CV
r
et )(
0
20
CV
r
.
Remarque : on pourra tracer au préalable le vecteur )()(
20
21
10
11
CVCV
r
r
− .
2.5 – En déduire )()()(
0
21
0
11
0
CVCVCV
r
r
r
==

INSA de Lyon Lundi 26 Janvier 2009
2ème année
4
3 – Etude des actions hydrodynamiques sur un propulseur.
3.1 - En vous appuyant sur les informations fournies en annexe (document 4), définir pour la
configuration neutre (figure 4a) les éléments de réduction en O
0
du torseur des actions
mécaniques exercées par l’eau sur le propulseur.
3.2 – A partir des résultats obtenus précédemment, préciser pourquoi il est indispensable
d’associer deux propulseurs tournant en sens inverse.
3.3 - En vous appuyant sur les informations fournies en annexe (document 4), tracer sur le
document 4 et pour la configuration de la figure 4b les actions mécaniques (portance et
traînée) en chaque point Pi.
Remarque : Par analogie avec les données de la figure 4a, on notera :
- T la norme de la traînée s’exerçant sur les pales 1 et 3
- P’ la norme de la portance et T’ la norme de la traînée s’exerçant sur les pales 2 et 4.
3.4 – Donner, pour la position du propulseur définie sur la figure 4b, les éléments de réduction
en O
0
du torseur des actions mécaniques exercées par l’eau sur le propulseur.
Remarque : Cette analyse est entreprise pour les positions :
- 0
=
β
du solide 31 supportant la pale 1
- 2/
π
β
=
du solide 32 supportant la pale 2
-
π
β
=
du solide 33 supportant la pale 3
- 2/3
π
β
=
du solide 34 supportant la pale 4
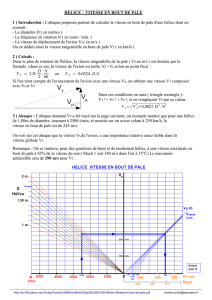
3.5 – En vous appuyant sur la courbe d’évolution de l’incidence présentée ci-dessous, préciser
la direction dans laquelle s’exerce l’effort hydrodynamique sur le propulseur.
Remarque : Pour les valeurs d’incidence présentée ci-dessus et pour un profil de pale
symétrique, il est légitime de considérer que la portance est proportionnelle à l’incidence.
3.6 – À partir des résultats obtenus précédemment, préciser la configuration de manœuvre
correspondant à la configuration de la figure 4b.
-15
-10
-5
0
5
10
15
0 90 180 270 360 450 540 630 720
Incidence (deg)
β(deg)

INSA de Lyon Lundi 26 Janvier 2009
2ème année
5
4 – Etude d’un mécanisme d’orientation à courroie
Un mécanisme d’orientation similaire à celui que nous venons d’étudier peut être obtenu à
l’aide d’un système poulie / courroie. Le mécanisme schématisé sur le document 5 en est une
version élémentaire.
Il est constitué des solides :
- 3 en liaison pivot d’axe ),(
3,00
zO
r
avec 0 Paramètre de mouvement : ),(
30
xx
r
r
= β
- 6 en liaison pivot d’axe ),(
6,3,0
zP
r
avec 3 Paramètre de mouvement : ),(
606
xx
r
r
= ϕ
La pale est solidaire du solide 6 et une courroie est montée entre deux poulies de rayon a
respectivement solidaires du bâti 0 et du solide 6.
4.1 – En traduisant la condition de non glissement en M entre la poulie liée à 0 et la courroie c,
calculer )(
3
MV
c
r
.
4.2 – Traduire la condition de non glissement en N entre la poulie liée à 6 et la courroie.
Remarque : la vitesse du point courant Q de la courroie est donné par : )()()(
333
NVMVQV
ccc
r
r
r
==
4.3 – Préciser la nature du mouvement du solide 6 par rapport au bâti 0.
4.4 – Préciser pourquoi cette architecture ne peut pas remplacer la précédente et proposer des
évolutions pour y parvenir.
4.5 – Donner la trajectoire du point M dans R
0
et calculer )(
0
MV
r
et )(
0
MJ
r