

A.3.2.4 Puissance en régime sinusoïdal
1°) Puissance instantanée
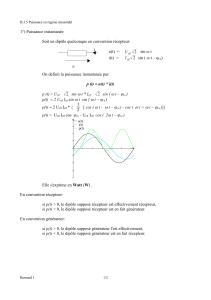
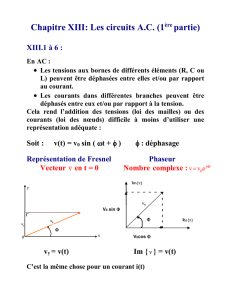
Soit un dipôle quelconque en convention récepteur:
u(t) =
Ueff 2
sin ω t
i(t) =
Ieff 2
sin ( ω t – ϕi/u)
On définit la puissance instantanée par:
p (t) = u(t) * i(t)
p (t) = Ueff
2
sin ω t * Ieff
2
sin ( ω t – ϕi/u)
p(t) = 2 Ueff Ieff sin ω t sin ( ω t – ϕi/u)
p(t) = 2 Ueff Ieff * {
1
2
[ cos ( ω t - ω t – ϕi/u ) - cos ( ω t + ω t – ϕi/u )]}
p(t) = Ueff Ieff cos ϕi/u - Ueff Ieff cos ( 2ω t – ϕi/u )
Elle s'exprime en Watt (W) .
En convention récepteur:
si p(t) > 0, le dipôle supposé récepteur est effectivement récepteur,
si p(t) < 0, le dipôle supposé récepteur est en fait générateur.
En convention générateur:
si p(t) > 0, le dipôle supposé générateur l'est effectivement,
si p(t) < 0, le dipôle supposé générateur est en fait récepteur.
Bernaud J 1/3
i
u
u(t)
i(t)
p(t)

A.3.2.4 Puissance en régime sinusoïdal
2°) Puissance apparente
Cette puissance n'est pas une grandeur physique au sens propre, c'est une grandeur de
dimensionnement. Elle se définit comme suit:
S = Ueff Ieff
La puissance apparente S s'exprime en Volt.Ampère (VA).
3°) Puissance active
3.1)Définition
La puissance active est la valeur moyenne de la puissance instantanée prise sur une
période.
P =
1
T∫ptdt
= Ueff I eff cos ϕi/u
P s'exprime en Watt ( W). Elle se mesure à l'aide d'un wattmètre.
3.2)Exemples
Pour une résistance parfaite :
PR = Ueff Ieff cos ϕi/u = Ueff Ieff = R Ieff2 ( ϕi/u = 0 rad)
Pour une inductance parfaite :
PL = Ueff Ieff cos ϕi/u = 0 W car ϕi/u = ( π / 2)
Pour un condensateur parfait :
PC = Ueff Ieff cos ϕi/u = 0 W car ϕi/u = (- π / 2)
4°) Puissance réactive ( valable uniquement en régime sinusoïdal)
4.1)Définition
La puissance réactive se définit ainsi: Q = Ueff Ieff sin ϕi/u
Elle s'exprime en volt ampère réactif (var).
Bernaud J 2/3
W
Réseau Installation
Bornes du
circuit courant
Bornes du
circuit tension

A.3.2.4 Puissance en régime sinusoïdal
4.2)Exemples
Pour une résistance parfaite :
QR = Ueff Ieff sin ϕi/u = 0 var ( ϕi/u = 0 rad)
Pour une inductance parfaite :
QL = Ueff Ieff sin ϕi/u = Ueff Ieff = L ω Ieff2 ,ϕi/u = ( π / 2)
L'inductance consomme de la puissance réactive.
Pour un condensateur parfait :
QC = Ueff Ieff sin ϕi/u = - Ueff Ieff = - Ueff2 C ω ,ϕi/u = (- π / 2)
Le condensateur fournit de la puissance réactive.
5°) Relations entre les puissances
S= P2Q2
et Q = P. tan(ϕi/u )
6°) Facteur de puissance
Par définition, le facteur de puissance est
k=P
S
En régime sinusoïdal et uniquement dans ce cas là: k = cos ϕi/u
7°) Théorème de Boucherot ( valable uniquement pour les régimes sinusoïdaux)
Il y a conservation de la puissance active et réactive.
La puissance active consommée par une association de n dipôles est égale à la somme
des puissances actives consommées par chaque dipôle.
P=∑
k=1
k=n
Pk=P1 P2 Pn
La puissance réactive consommée par une association de n dipôles est égale à la
somme des puissances réactives consommées par chaque dipôle.
Bernaud J 3/3
Q=∑
k=1
k=n
Qk=Q1 Q2 Qn