Petits problèmes au quotidien

P§fîfS PI IS iu ciuûttdiiin
1 vil 1, Sf/ W1
Christian Boissinotte, CSDM
m^j Mi Vli Mj w t ^ 1ttf
Traduction et adaptation de problèmes tirés de la revue
1 vil 1, Sf/ W1
Christian Boissinotte, CSDM Mathematics
Teacher, mai 1999
figure numéro 1
KJ
figure numéro 2
figure numéro 3
figure numéro 4
Albert (16)
Frank (10)/ \Benoit(8)
Éliane (8) 'Carole (12)
Denis (12)
figure numéro 10
Solutions à la page : 44
1. Un cercle est circonscrit à un triangle équilatéral et un autre cercle est inscrit
dans ce même triangle. Quel est le rapport des aires du grand au petit cercle?
(voir figure)
2. Un hexagone régulier est inscrit dans un cercle. Un autre hexagone
régulier est circonscrit au cercle de façon que le centre de chacun de ses côtés
coïncide avec un sommet du premier hexagone. Quel est le rapport des aires du
grand hexagone au petit? (voirfigure)
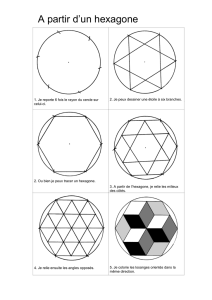
3. Chaque côté d'un hexagone régulier est prolongé d'une mesure égale à la sienne,
et les extrémités de ces segments sont reliées pour former un nouvel hexagone.
Donnez le rapport des aires du grand hexagone au petit, (voirfigure)
4. Un triangle rectangle isocèle ABC, dont les cathètes mesurent un décimètre
chacun est découpé dans une feuille de papier blanche d'un côté et noire de
l'autre. Le coin C est replié le long du côté CB de façon que les parties visibles
noires et blanches soient de même aire. Après le pliage, à quelle distance doit
être le point C du coin B? (voirfigure)
5. . Un cheval de bois monte et descend de 30 cm exactement huit fois à chaque
tour complet d'un manège. Si le cheval commence à monter au début de la
révolution du carrousel, à quel hauteur sera-t-il après deux-tiers de tour? Sera-
t-il en train de monter ou de descendre?
6. Daniel se tient dans un trou de 120 cm de profond. Il dit qu'en creusant encore 125
cm, le dessus de sa tête sera à la même distance sous le sol qu'elle l'est maintenant
au-dessus du sol. Quelle est la grandeur de Daniel ?
7. A, B, C, D et E représentent cinq chiffres différents. Que vaut B + D, sachant
queA + B = CetC-i-D = EA?
8. Une boîte contenait 31 chocolats. La première journée, Gabriel a mangé les —
4
de ce que Pamela a mangé. Le lendemain, Pamela mange une fois et demie ce
que mange Gabriel, et il ne reste plus de chocolat! Combien de chocolats
Gabriel a-t-il mangé?
9. David traverse un tunnel de huit kilomètres en auto. À ce moment précis, quelle
est la probabilité qu'il soit à au moins six kilomètres de l'une des extrétiiités du
tunnel?
10. Albert, Benoit, Carole, Denis, Éliane et Frank forment un cercle. Chacune de
ces personnes choisit un nombre et le dit à ses deux voisins immédiats. En-
suite, chaque personne annonce la moyenne des nombres de ces deux mêmes
voisins (nombres sur la figure). Quel nombre avait choisi Denis? (voirfigure)
11. Si 100 est divisé par un certain nombre naturel, le reste est 2. Si on divise 198
par ce même nombre, quel sera le reste?
8 ENVOJL
NO 119 - AVRIL-MAt-JUlN 2002 8

Sotuttûis des petits pmltèmis
Christian Boissinotte, CSDM
figure numéro 1
1. 4.
On voit que R = 2r, car R est la mesure de l'hypothénuse d'un triangle 30°-
6G°- 90° et r est celle du côté opposé à l'angle de 30°. Le rapport des
rayons est 2, donc le rapport des aires est le carré de ce rapport, soit 4.
(voir figure)
2. t
figure numéro 2
figure numéro 3
On sait que le rapport des aires est le carré du rapport des apothèmes,
— .Par contre, on remarque que l'angle illustré est de 30°, ce qui
a
entraîne que a = —A. Le rapport des aires est donc —.
S
—A. Le rapport aes aires est aonc ^
(voir figure)
3. 3.
Chaque angle extérieur au petit hexagone régulier, en particulier entre
les côtés dont les mesures c et 2c sont indiquées sur la figure, est de
360° 6 ou 60°. Par la loi des cosinus, on trouve que le troisième côté
est cV3. En effet, c^ + {Icf -l-c.-lc-cos60°=3c2en est le carré.
Le rapport des aires est le carré du rapport des côtés, soit
(voir figure)
4. 0,26 dm.
\2
C
V
figure numéro 4
Le rapport des aires du triangle CAB au triangle CDC est -. Puisque
le rapport des aires de ces triangles semblables est le carré du rapport
^ [2 /- 2V3 ,
- X V2 = donc
^3 3
des longueurs, on a que mCC = mBC =
mBC = V2 - 2S 0,26 dm. (voirfigure)
5. 20 cm.
2 1
de 8 représente 5- cycles. Le cheval monte et descend cinq fois
puis parcourt un tiers de cycle. Il monte car il n'a pas atteint la moitié
du cycle. Si on pense que le mouvement d'ascension est linéaire,
44 ENVOJL
NO 119 - AVRIL-MAt-JUlN 2002 44

30 cm Jl. un cycle
„// \\ ISd-cosW)
/f
/!
/ /
\\
231
figure numéro 5
2é
on dira que la hauteur atteinte par rapport au point le plus bas est - de
30 cm, SOit 20 cm. (voirfigure)
Remarque : II est plus probable que le mouvement soit sinusoïdal, auquel
cas on peut utiliser la fonctions suivante.
f
15(1-cos — )= 15 X 1,5 = 22,5 cm au-dessus du point le plus bas.
V 3 y
6. 182,5 cm.
Soit j: la grandeur de Daniel. Il dépasse de x - 120 centimètres. Après
avoir creusé, sa tête sera à 245 - x centimètres sous le sol. Puisque ces
deux quantités sont égales, on a x - 120 = 245 - ;c ou 2x = 365 et x =
182,5 cm.
7. A, B, C, D et E représentent cinq chiffres différents.
E = 1 nécessairement. En remplaçant, ona(A-i-B) + D=10 + A, donc
B+D=10.
8. 13 chocolats.
Soit p^ ce que Paméla a mangé la première journée et p^la deuxième
3 2
journée. Gabriel a mangé —P\ + -P2 Paméla +p^.
Le total, = Considérant que les deux termes doivent être
entiers, il faut trouver un multiple de 4 et un multiple de 3. La seule
possibilité est = 12 et = 6. Paméla à donc mangé 18 chocolats et
Gabriel le reste, soit 13.
9. A
Il serait alors dans les deux premiers ou les deux derniers kilomètres du
tunnel, ce qui constitue en tout la moitié de la longueur du tunnel.
10. 4.
Symbolisons le nombre choisi par chaque personne par l'initiale de son
nom.
D + 5 = 24, 5-I-F = 32 et F-I-D = 16.
En remplaçant 5, on a D + ( 32 - F ) = 24 ou D - F = -8
En ajoutant F-i-D=16etD-F=-8 membre à membre, on a 2D = 8 ou
D = 4.
11. 2.
Soit X ce nombre. Il existe un nombre t tel que 100 = xf -i- 2 et aussi
98 = xM98 = 100 -I- 98 = 2xt + 2. Donc 198 divisé par x donne 2t et le
reste est 2.
ENVOJL NO 119 - AVRIL-MAt-JUlN 2002 45