pondichery - Numeriksciences

numeriksciences.fr ©copyright AMERIQUE DU NORD 2016
Page 1 sur 3
Exercice 2 : DETECTION ET HABITABILITE D’UNE EXOPLANETE
(5 points)
1. Illustration du principe de détection par vélocimétrie
1.1. Démarche des chercheurs
Les chercheurs ont mesuré à plusieurs reprises la valeur de λmesurée d’une raie du spectre
de l’étoile. Ils en ont déduit le décalage Δλ en faisant la différence entre le λ de référence
de cette même raie étudiée sur Terre. Puisque la vitesse v dépend de ce décalage ils en
ont déduit la vitesse v telle que : v = c × Δλ / λ puis ont tracé v au cours du temps.
1.2. Période de révolution de l’étoile et de l’exoplanète
Echelle axe horizontal = échelle axe des temps : 5 sous divisions = 1 jours
Pour 3 périodes T : il y a 33 sous divisions d’où 3T = 33/5 il vient T = 33 / (3 × 5) = 2,2 jours
La période de l’étoile est de 2,2 jours soit 1,9 × 105s. L’exoplanète constitue avec l’étoile le
système, l’exoplanète a aussi une période de 2,2 jours.
1.3. Nature de la trajectoire de l’exoplanète
Le graphe montre une courbe sinusoïdale donc le mouvement est circulaire.

numeriksciences.fr ©copyright AMERIQUE DU NORD 2016
Page 2 sur 3
1.4. Mouvement uniforme de l’exoplanète
L’exoplanète tourne autour de l’étoile à une distance D. Elle subit une force gravitationnelle
telle que
(avec  le vecteur unitaire allant de l’étoile vers l’exoplanète)
Deuxième loi de Newton : 
   donc 
Le vecteur force gravitationnelle  est alors dans le même sens que le vecteur accélération
.
Le vecteur accélération est radial, dans le repère de Frênet, donc l’accélération tangentielle
at est nulle. Or 
 donc cela signifie que v = constante. Le mouvement est donc
uniforme.
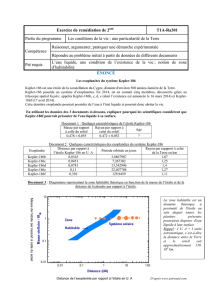
2. Habitabilité de l’exoplanète du système HD189733
2.1. Troisième loi de Kepler
Pour toutes les planètes le rapport entre le carré de la période et le cube du demi
grand axe est le même (égal à une même constante).
tetancons
a
T
3
2
2.2. Relation entre T2 et R3
Pour un mouvement circulaire a = R rayon de la trajectoire circulaire.
La 3ème loi de Kepler devient :
tetancons
R
T
3
2
.
D’après la deuxième loi de Newton :    donc Fg = M × an = M × v2 / R
an : accélération normale
D’où :  
=   =  = 
or:   
 il vient : 
= 
d’où :
et
3MG
²4
R
²T
2.3. Distance moyenne entre l’étoile et l’exoplanète
On isole R3 : R3 =
²4
²TMG

numeriksciences.fr ©copyright AMERIQUE DU NORD 2016
Page 3 sur 3
 R =
3
53011
3
²4
²109,110989,182,01067,6
²4
²TMG
 R = 4,6 × 109 m = 4,6 × 109 / 1,50 × 1011 = 3,1 × 10-2 U.A
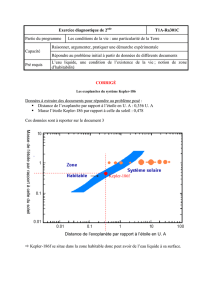
La distance est inférieure à 0,726 U.A. Les conditions ne sont pas bonnes et ne se
trouve pas dans la zone d’habitabilité. L’exoplanète doit recevoir trop de puissance par
mètre carré de la part de l’étoile.