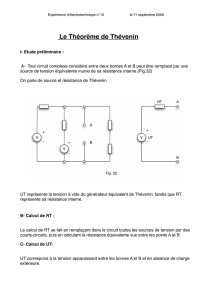
E2.9. Résistance itérative. 1. Valeur du résistor R`. On souhaite que

www.kholaweb.com
E
2.9. Résistance itérative.
1.
Valeur du résistor
R
’.
On souhaite que
'
AB
R R
.
Or cette résistance s’exprime
par
2 '
3 '
AB
R R R
R
R R
. On obtient ainsi l’égalité
:
2 2
2 2
2 2
2 '
' 2 ' 3 ' '
3 '
2 2 ' '
' 2 ' 2 0
R R R
R R RR RR R
R R
R RR R
R RR R
On résout cette
équation du second degré
et on ne garde que la racine positive
:
2
' 3 ' 3 1
R R R
2.
Résistance du réseau.
Considérons un circuit qui présenterait l’association de deux modules sur la résistance
R
’. En tenant compte
du résultat de la question
précédente, on a les montages équivalents suivants
:
La résistance équivalente ne dépend pas du nombre
n
de modules. On peut montrer cela par récurrence. On
suppose la propriété vraie pour
n =
1 et
n
= 2 et on la suppose vraie pour
n
–
1. Pour l’ordr
e
n
:
On se retrouve dans le cas du réseau où
n
= 1.
La résistance équivalente du réseau constitué des
n
modules et de la résistance
R
’ est égale
à
' 3 1
AB
R R R
.
On appelle cette résistance
R’
résistance itérative.
www.kholaweb.com

3. Tension
u
aux bornes
de
R
’.
On considère un couple
,
i i
A B
. La résistance équivalente à la partie droite de ce couple est
R
’. On calcule
alors en utilisant la notion de pont diviseur de tension la tension
1
i
u
en fonction de la tension
i
u
:
On obtient
:
1
'
2 '
i i
R
u u
R R
Soit
:
2
1 2 1
' ' ' '
, , ... ,
2 ' 2 ' 2 ' 2 '
3 1
3 1
n
o o n o
n
n o
R R R R
u u u u u u u
R R R R R R R R
u u
www.kholaweb.com