TS Physique Un ballon stratosphérique Exercice résolu

Page 1 sur 4
Un ballon stratosphérique Document : M.Moppert – CPF - Beyrouth
- Enoncé –
Un ballon stratosphérique, utilisé pour les relevés météorologiques, est constitué d'une enveloppe en latex
renfermant de d'hélium (gaz de densité inférieure à 1) et d'une nacelle. Celle-ci abrite différents capteurs (de
température, de pression, ...), ainsi qu'un émetteur radio qui transmet au sol les résultats des mesures pendant
le vol.
Données :
• La masse du système {ballon + nacelle + corde} est m = 8,0 kg.
• L'enveloppe de latex sera considérée comme une sphère :
- de rayon r = 1,3 m, supposé constant pendant toute la durée du vol (première et deuxième parties),
- de volume noté Vb
3
b
4
V .r
3
= π .
• Valeur du champ de pesanteur : g = 9,8 m.s-2.
• La densité d’un gaz est le rapport entre sa masse volumique ρ et la masse volumique de l’air ρ0.
Le but de l’exercice est de déterminer, à chaque instant, la valeur de la vitesse instantanée du ballon lors de son
ascension. Après avoir réalisé l’étude dynamique de la situation (première partie), la méthode de calcul itératif
d’Euler permettra de calculer la vitesse instantanée d’ascension du ballon (deuxième partie). La comparaison de
cette étude avec les données d’un vol réel est proposée en troisième partie.
A. Première partie : Étude dynamique
Concernant la poussée d'Archimède et les frottements dus à l'air, seules seront prises en compte les forces
s’exerçant sur le ballon (celles s’exerçant sur la corde et la nacelle sont négligeables).
Le ballon stratosphérique sera représenté par un point M, correspondant au centre d'inertie de l'ensemble. Le
mouvement du ballon sera étudié sur un axe (Oy) vertical, dirigé vers le haut, muni d’un vecteur unitaire
j
.
A t = 0 s, le point M se trouve en O et le ballon est alors lâché sans vitesse initiale. On notera vy la composante
de la vitesse sur l'axe (Oy), et ay la composante de son accélération sur ce même axe.
On choisit de modéliser la valeur de la force de frottement par f =
1
2
ρo.CX.S.v² (modèle turbulent).
-3
0 0
X X
2
, la masse volumique de l'air : = 1,22 kg.m
C , le coefficient de traînée : C = 0,70 unités S.I.
avec S, la surface offerte par la section du
ballon : S = .r
v, la valeur de la vitesse
ρ ρ
π
1. Faire une étude dimensionnelle afin de déterminer l’unité S.I de CX.
2. a) Faire le bilan des différentes forces extérieures s'appliquant sur le système {ballon + nacelle + corde}.
Les représenter sur un schéma.
b) Écrire les expressions vectorielles de ces forces en fonction des données de l’énoncé.
3. a) Montrer que le mouvement du ballon obéit à l'équation différentielle :
= − +
y2
y
dv
A.v B
dt , où A et B sont des
constantes dont les expressions littérales sont : A = 0 X
.C .S
2m
ρ
et B = 0b
.V
g. 1
m
ρ
−
b) Calculer les valeurs des constantes A et B.
4. a) En s’appuyant sur le bilan des forces, expliquer pourquoi la vitesse du ballon atteint une valeur limite vlim.
b) Établir l’expression littérale de vlim et calculer sa valeur.
TS
Physique
Un
b
allon stratosphérique
Exercice résolu

Page 2 sur 4
Un ballon stratosphérique Document : M.Moppert – CPF - Beyrouth
B. Deuxième partie : Calcul de la vitesse instantanée
On utilise la méthode d'Euler avec un pas δt = 0,25 s.
On appellera vn la valeur de la vitesse du ballon à l'instant tn, et vn+1 la valeur de sa vitesse à l'instant tn+1 = tn +
δt. On aura alors δv = vn+1 – vn.
1. Déduire de l’expression de l’équation différentielle la relation de récurrence :
vn+1 = vn.(1– 0,070.vn) + 1,0 (unités S.I)
2. Un tableur a permis de calculer l'évolution de la vitesse entre t = 0,0 s et t = 3,0 s. Les résultats sont
rassemblés dans le tableau ci-dessous :
tn (s) 0,00 0,25 0,50 0,75 1,0 1,25 1,50 1,75 2,0 2,25 2,50 2,75 3,0
vn(m.s-1) 0,0 1,0 1,9 2,6 3,4 3,6 3,7 3,7 3,7 3,7
Calculer la vitesse du ballon aux dates tn égales à : 1,0 s, 1,75 s et 3,0 s.
3. La valeur de la vitesse limite est-elle en accord avec la valeur trouvée en première partie ?
C. Troisième partie : Profil du vol réel
Jusqu’ici, le volume de l’enveloppe de latex a été considéré constant. En fait, lors de la montée, la pression
atmosphérique diminue (la masse volumique de l’air diminue) et, par conséquent, le volume et le surface de
l’enveloppe augmentent. Il s’ensuit une évolution de la poussée d’Archimède et des forces de frottements.
En général, aux alentours de 35 km d’altitude, le ballon finit par éclater. Il redescend, sa chute étant freinée
par l’ouverture d’un petit parachute.
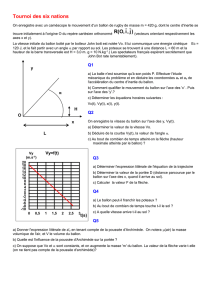
Le diagramme ci-dessous reconstitue un profil de vol à partir des mesures (sur ce diagramme, on a tracé la
tangente à la courbe à la date t = 2,75 h) :
1. a) Comment évolue la vitesse ascensionnelle ? Justifier
graphiquement.
b) Expliquer brièvement quelles sont les forces responsables
de cette évolution.
c) En considérant l’échelle des temps, dire si l’observation est
en accord avec l’évolution donnée en parties 1 et 2.
2. En appuyant le raisonnement sur le dispositif de chute,
proposer une explication à l’évolution de la vitesse lors de la
descente vers le sol.
3. Évaluer la valeur de la vitesse de la nacelle lors de son impact sur le sol.
(T)

Page 3 sur 4
Un ballon stratosphérique Document : M.Moppert – CPF - Beyrouth
- Corrigé –
A. Première partie : Étude dynamique
1. Faire une étude dimensionnelle afin de déterminer l’unité S.I de C
X
.
D’après le théorème du centre d’inertie : [f] = M.L.T-2
Le modèle de la force de frottement conduit à : [CX] =
[ ]
[ ]
2
2 2 3 2 1 2
0 0
f f M.L.T
.S.v .S.v M.L .L .(L.T )
−
− −
= =
ρ ρ
  = 1
CX est donc un nombre sans dimension.
2. a) Faire le bilan des différentes forces extérieures s'appliquant sur le système {ballon
+ nacelle + corde}. Les représenter sur un schéma.
b) Écrire les expressions vectorielles de ces forces en fonction des données de l’énoncé.
Bilan des forces et expressions vectorielles :
P
(poids du système),
A
F
(poussée
d’Archimède) et
f
(force de frottement).
Par projection dans le repère choisi :
y
P P .j
= avec Py = - P = - m.g =>
P m.g.j
= −
AAy
F F .j
= avec FAy = FA = ρ0.V0.g => A0 0
F .V .g.j
= ρ
y
f f .j
= avec fy = - f = -
2
0 x
1
. .C .S.v
2
ρ => 2
0 x
1
f . .C .S.v .j
2
= − ρ
3. a) Montrer que le mouvement du ballon obéit à l'équation différentielle
= − +
y2
y
dv
A.v B
dt
, où A et B sont des constantes dont
les expressions littérales sont : A =
0 X
.C .S
2m
ρ
ρρ
ρ
et B =
0 b
.V
g. 1
m
ρ
ρρ
ρ
−
−−
−
Référentiel : terrestre supposé galiléen.
Système : {ballon + nacelle}.
2ème loi de Newton s’écrit : ext A
M
F P F f m.a
= + + =
∑
.
Projection dans le repère (O,
j
) : Py + FAy + fy = m.aMy => -m.g + ρ0.Vb.g -
1
2
.ρ0.CX.S.vy2 = m.aMy = m.
y
dv
dt
On obtient finalement :
= − +
y2
y
dv
A.v B
dt avec A = 0 X
.C .S
2m
ρ
et B = 0 b
.V
g. 1
m
ρ
−
b) Calculer les valeurs des constantes A et B.
A =
2
1,22 0,70 (1,3)
2 8,0
× × π ×
×= 2,8 x 10-1 m-1 et B = 3
1,22 4 (1,3)
9,8 1
3 8,0
× π ×
× −
×
= 4,0 m.s-2
4. a) En s’appuyant sur le bilan des forces, expliquer pourquoi la vitesse du ballon atteint une valeur limite v
lim
.
La vitesse initiale est nulle. Dès le début du mouvement, la vitesse augmente : la poussée d’Archimède, orientée
dans le sens du mouvement, est responsable de cette évolution.
Cependant, lorsque la valeur de la vitesse augmente, la valeur de la résultante des forces de frottements
augmente. Il s’ensuit que, pour une certaine vitesse vlim, la poussée d’Archimède est entièrement compensée par
le poids et les forces de frottements : le mouvement de M est alors rectiligne uniforme.
b) Établir l’expression littérale de v
lim
et calculer sa valeur.
Le mouvement s’effectuant à vitesse constante : ay =
y
dv
dt
= 0 => vy =
B
A
Soit : vy =
4,0
0,28
= 3,8 m.s-1.
O
M
j
y
A
F
P
f
g

Page 4 sur 4
Un ballon stratosphérique Document : M.Moppert – CPF - Beyrouth
B. Deuxième partie : Calcul de la vitesse instantanée
1. Déduire de l’expression de l’équation différentielle la relation de récurrence : v
n+1
= v
n
.(1– 0,070.v
n
) + 1,0 (unités S.I)
Soit δt un intervalle de temps suffisamment petit pour pouvoir écrire :
t
v(t t) v(t)
dv
dt t
=+ δ −
  δ
  => 2
v(t t) v(t)
A.(v(t)) B
t
+ δ −
= − +
δ.
En posant : v(t + δt) = vn+1 et v(t) = vn, on obtient la relation de récurrence : vn+1 = vn – A.
2
n
v
.δt + B.δt
Numériquement, et avec un pas de calcul δt = 0,25 s, on obtient : vn+1 = vn.(1– 0,070.vn) + 1,0 (unités S.I)
2. Calculer la vitesse du ballon aux dates t
n
égales à : 1,0 s, 1,75 s et 3,0 s.
En utilisant la relation de récurrence précédente, il vient :
v4 = v3 (1 – 0,070.v3) + 1,0, soit avec v3 = 2,6 m.s-1 : v4 = 3,1 m.s-1
v7 = v6 (1 – 0,070.v6) + 1,0, soit avec v6 = 3,6 m.s-1 : v7 = 3,7 m.s-1
v12 = v11 (1 – 0,070.v11) + 1,0, soit avec v11 = 3,7 m.s-1 : v12 = 3,7 m.s-1
3. La valeur de la vitesse limite est-elle en accord avec la valeur trouvée en première partie ?
La vitesse limite est ici égale à 3,7 m.s-1, valeur à comparer à 3,8 m.s-1 trouvée précédemment. Les deux valeurs
sont très proches, les deux méthodes (analytique et itérative) conduisent au même résultat.
C. Troisième partie : Profil du vol réel
1. a) Comment évolue la vitesse ascensionnelle ? Justifier graphiquement.
La pente de la tangente à la courbe augmente au cours du temps : la vitesse augmente.
b) Expliquer brièvement quelles sont les forces responsables de cette évolution.
Seule la poussée d’Archimède est orientée dans le sens du mouvement. Elle seule permet d’expliquer cette
évolution. La densité de l’air diminue, le volume du ballon augmente. La poussée d’Archimède n’est à priori plus
constante comme en première partie. L’augmentation de la vitesse nous permet d’affirmer que la valeur de la
poussée d’Archimède est, tout au long de la montée, supérieure à la norme du poids et de la résultante des
forces de frottements réunies.
c) En considérant l’échelle des temps, dire si l’observation est en accord avec l’évolution donnée en parties 1 et 2.
En deuxième partie, la vitesse limite était atteinte au bout de 1,75 s. C’est-à-dire qu’il était légitime d’affirmer
que la quasi-totalité du mouvement s’effectuait à vitesse constante. La courbe donnée du vol réel nous amène au
contraire à affirmer qu’aucune vitesse limite n’est atteinte ; la vitesse augmente jusqu’au sommet de la
trajectoire.
Cependant, ces deux affirmations n’entrent pas en contradiction puisque le modèle descriptif du système n’est
pas le même dans les deux cas : en première partie, le ballon est considéré de volume constant et l’air, de
densité constante, alors que ce n’est plus le cas dans cette troisième partie.
2. En appuyant le raisonnement sur le dispositif de chute, proposer une explication à l’évolution de la vitesse lors de la descente
vers le sol.
Au cours de la descente, on constate que la vitesse diminue (la pente de la tangente à la courbe diminue). En
effet, le parachute se trouve de plus en plus freiné à mesure qu’il descend puisqu’il rencontre des couches d’air
de plus en plus denses.
3. Évaluer la valeur de la vitesse de la nacelle lors de son impact sur le sol.
La valeur de la vitesse recherchée est égale à la valeur absolue du
coefficient directeur de la tangente à la courbe au moment de
l’impact. On utilise les points A et B de coordonnées respectives
(tA ; zA) et (tB ; zB) pour calculer cette vitesse, notée vimpact :
vimpact = B A
B A
z z
0 30
t t 2,75 1,5
−−
=
− − = 24 km.h-1 ou 6,7 m.s-1
A
B
A
B