Nom / prénom :

Page n°1 Contrôle n°4
NOM :
Contrôle n°4
55 min
Seconde 13
13 / 12 / 2010
L'usage de la calculatrice est interdit !
Exercice n°1 : "Sur les traces du diamant bleu" (15 points et 2 points de bonus).
Donnée : la charge élémentaire e vaut : .
Les extraits paru dans la revue Pour la Science
n°398 de décembre 2010.
"Les caractéristiques optiques et cristallographiques du plus gros diamant bleu connu disparu au XVIIe siècle ont été reconstituées grâce
1. "Le diamant est un minéral de la famille des « natifs -à-dire composé essentiellement
te et de
bore peuvent lui donner diver
"
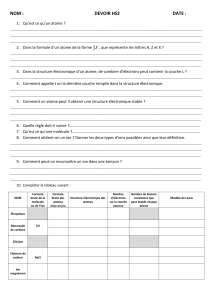
1.1. Le numéro atomique de l'élément carbone est 6. La variété la plus répandue possède 12 nucléons. Donner la composition de
l'atome de carbone, ainsi que la notation symbolique de son noyau.
1.2. Une des variété du carbone possède 14 nucléons. Quelle différence cela induit-il dans la composition de l'atome de carbone ?
Donner alors la notation symbolique de son noyau. Comment nomme-t-on les deux variétés de l'élément carbone ?
1.3. Donner la structure électronique de l'atome de carbone. Combien d'électrons externes possède l'atome de carbone ?
1.4. (Bonus) L'élément bore se situe ligne 2 et colonne 13 dans la classification périodique des éléments. En déduire sa structure
électronique et son numéro atomique.
2. "La découverte d'un diamant en surface tient presque du miracle, tant les conditions à réunir sont rares. Formés dans les profondeurs du
manteau terrestre, les diamants
45%), du magnésium et sont riches en fluides (H2O et CO2) et en potassium."
2.1. Donner les noms des deux fluides contenus dans les kimberlites.
2.2. Dans les kimberlites l'élément magnésium de symbole Mg et de numéro atomique 12, se trouve sous la forme d'ion de symbole
Mg2+. Combien d'électrons possède l'ion magnésium ? Justifier votre réponse. En déduire sa configuration électronique.
2.3. Les silicates sont formés en particulier à partir des éléments silicium (Si) et oxygène (O). L'élément oxygène peut être sous forme
d'ion de charge globale égale à . Donner la formule de cet ion en la justifiant. Cet ion est-il un cation ou un anion ?
2.4. L'élément potassium a pour symbole
. Donner la structure électronique de l'atome de potassium.
3. Étude de la seconde loi de Snell-Descartes relative à le réfraction dans un diamant.
"Une conséquence de cette loi est que, quel que soit l'angle d'incidence de la lumière sur le diamant, l'angle du rayon réfracté ne dépasse
pas une valeur critique (pour le diamant, 26° par rapport à la verticale de la facette éclairée). De même, si la lumière traversant le
diamant arrive sur une facette avec un angle supérieur à la valeur critique, elle est réfléchie dans le diamant, comme si la facette était un
miroir [...]. À l'opposé, si l'angle d'incidence est inférieur à l'angle critique, la lumière sort du diamant et repasse dans l'air. Ainsi les
facettes d'un diamant taillé sont combinées de telle manière que la lumière soit piégée dans le diamant et ne puisse s'échapper que vers
les observateurs. Par conséquent, le diamant apparaîtra très lumineux."
3.1. Choisir en le justifiant le schéma adapté à la description du phénomène de réfraction pour l'angle d'incidence critique (ou limite).
Préciser sur le schéma choisi les milieux diamant (d'indice de réfraction n) et air (d'indice de réfraction n') et les angles
d'incidence ic et de réfraction i2 .
a. b. c. d.
3.2. (Bonus) Comment s'appelle le phénomène lorsque la lumière "arrive sur une facette avec un angle supérieur à la valeur critique" ?
3.3. En utilisant la seconde loi de Snell-Descartes relative à la réfraction écrire la relation littérale qui permet de calculer la valeur de
l'angle critique ic en fonction de n et n'.
3.4. Incidence de la taille sur la capture et le renvoi de la lumière.
3.4.1. Choisir, sans justification, le schéma permettant de réaliser les conditions du paragraphe 3 pour une taille idéale.
a. b. c.
3.4.2. Comment arrive la lumière sur la première face de chaque diamant ?
4. Compléter la phrase suivante sans utiliser deux fois le même mot :
"Le diamant en outre la lumière, car son varie de 2,451 dans le bleu à 2,407 dans le rouge. Ainsi,
la lumière sera fortement (effet de prisme ou d'arc-en-ciel) dans le diamant, créant les fameux « feux du diamant »."
Eh ben moi je
préfère avec !

Page n°2 Contrôle n°4
Exercice n°2 : avoir du plomb dans l'aile (10 points et 2 points de bonus).
Le plomb est un élément lourd très toxique pour l'homme est les animaux. En effet une intoxication au plomb, appelée saturnisme, induit
des troubles systémiques qui, selon leur gravité et le moment de l'intoxication, seront réversibles (anémie
irréversibles et éventuellement fatals (atteinte du système nerveux), stérilité, cancers, hypertension, puis encéphalopathie et paralysie
conduisant à la mort.
Voilà pourquoi : « À compter de la date d'ouverture de la chasse aux oiseaux de passage et au gibier d'eau en
2005, l'emploi de la grenaille de plomb (est interdit pour la chasse de tout gibier et pour la destruction des
animaux nuisibles) dans les zones humides suivantes :
en zone de chasse maritime ;
dans les marais non asséchés ;
sur les fleuves, rivières, canaux, réservoirs, lacs, étangs et nappes d'eau.
Le tir à balle de plomb du grand gibier demeure autorisé sur ces zones. »
Arrêté du 21 mars 2002 publié au Journal Officiel du 4 avril 2002.
Une cartouche de chasse contient environ 32 g de grenaille de plomb réparti en 200 billes approximativement sphériques.
Données :
Le volume V d'une sphère de rayon r est donné par la relation :
.
La charge élémentaire e vaut : .
La couche n contient 2n² électrons ( pour la couche K, etc.).
Masse d'un nucléon : .
Aides au calcul :
;
;
Rayon de l'atome de plomb : ;
La masse volumique µ (en kg.m-3) est donnée par la relation :
; où m
s'exprime en kg et V en m3.
; .
1. :
. En déduire la composition de son
noyau.
2. (Bonus) Compléter la structure électronique de l'atome de plomb, sachant qu'il respecte le principe de construction :
KLMNO18P
3. en perdant deux électrons.
3.1. ? Justifier votre réponse.
3.2. Exprimer la charge du noyau de cet ion, puis celle de son nuage électronique en fonction de la charge élémentaire e.
3.3. En déduire sa charge globale en fonction de e, puis calculer sa valeur en Coulomb. Donner alors la notation complète de l'ion
plomb.
4. En utilisant les données de l'énoncé calculer au décigramme près la masse m d'une bille de plomb.
5. Montrer que la masse d'un atome de plomb ma est d'environ .
6. En déduire le nombre N d'atomes de plomb contenus dans une bille de plomb.
7. Donner l'ordre de grandeur du rayon de l'atome de plomb. En déduire le volume approché Va de l'atome de plomb.
8. (Bonus) Montrer alors que la masse volumique du plomb est d'environ 102 g.cm3.
9. (Bonus) En France il y a environ 1,5 million de chasseurs. Si chacun utilisait une seule cartouche par an, quelle quantité de plomb serait
déversée par les chasseurs dans la nature ? Exprimé le résultat en tonnes.
Non !
Oui !
Bon, long et dur celui-là ?
Allez, promis pour 2011 je
Passez de joyeuses fêtes !!!
Alors justifié cet arrêté ???

Page n°3 Contrôle n°4
Correction
Exercice n°1 : [15+2]
1. Les éléments carbone et bore.
1.1. L'atome de carbone possède :
6 protons (correspond au numéro atomique Z) ;
6 neutrons (possède 12 nucléons, notés A ; soit Z protons et N neutrons ; d'où : ) ;
et 6 électrons car l'atome est électriquement neutre.
La notation symbolique de son noyau est :
. [2]
1.2. L'atome de carbone-14 possède 8 neutrons au lieu de 6 pour le carbone-12. La notation symbolique de son noyau est :
. Les
atomes de carbone-12 et de carbone-14 sont des isotopes. [1,5]
1.3. La structure électronique de l'atome de carbone est : K2L4. Il possède 4 électrons externes. [1]
1.4. L'élément bore est situé sur la deuxième ligne, donc il possède deux couches (K et L). Comme il est colonne 13 il possède trois
électrons périphériques, donc sa structure électronique est : K2L3 et son numéro atomique est 5. [1,5]
2. Étude des kimberlites.
2.1. Les kimberlites contiennent de l'eau (H2O) et du dioxyde de carbone (CO2). [1]
2.2. L'ion magnésium possède 10 électrons. En effet un atome étant électriquement neutre il possède autant de protons que d'électrons
donc 12 pour l'atome de magnésium car : . L'ion magnésium possède deux charges excédentaires positives, donc il a perdu 2
électrons, il ne lui reste donc que 10 électrons . Sa configuration électronique est donc : K2L8. [2]
2.3. L'ion oxygène possède deux charges négatives excédentaires car :
; donc sa formule est : C'est un anion. [1,5]
2.4. La structure électronique de l'atome de potassium est : K2L8M8N1. [1]
3. Étude de la seconde loi de Snell-Descartes relative à le réfraction dans un diamant.
3.1. Le schéma adapté à la description du phénomène de réfraction pour l'angle d'incidence critique (ou limite) est le schéma d. [1,5]
3.2. Lorsque la lumière "arrive sur une facette avec un angle supérieur à la valeur critique" elle subit le phénomène de réflexion totale.
[0,5]
3.3. D'après la seconde loi relative à la réfraction : ; on a, avec les notations de l'énoncé : ;
or si l'angle d'incidence est égal à l'angle critique alors l'angle de réfraction i2 vaut 90°, d'où : ; donc :
; soit :
. [1,5]
3.4. Incidence de la taille sur la capture et le renvoi de la lumière.
3.4.1. Le schéma permettant de réaliser une taille idéale est le schéma b. [0,5]
3.4.2. La lumière arrive sous incidence normale sur la première face de chaque diamant. [0,5]
4. "Le diamant disperse en outre la lumière, car son indice varie de 2,451 dans le bleu à 2,407 dans le rouge. Ainsi, la lumière sera
fortement décomposée (effet de prisme ou d'arc-en-ciel) dans le diamant, créant les fameux « feux du diamant »." [1]
Exercice n°2 : [10+2]
1. Le noyau de l'élément plomb contient 82 protons et 126 neutrons (soit 208 nucléons). [1,5]
2. La structure électronique de l'atome de plomb est : K2L8M18N32O18P4. [1]
3. en perdant deux électrons.
3.1.
80. L'ion plomb possède donc 80 électrons. [1]
3.2. La charge du noyau est de : et celle de son nuage électronique : . [1]
3.3. Sa charge globale est donc : ; soit : . La natation complète de l'ion plomb est donc :
.
En effet : . [1,5]
4. La masse d'une bille de plomb est de 0,2 g. En effet 200 billes de plomb ont une masse de 32 g ; donc la masse d'une bille de plomb est
de :
[1]
5. La masse approchée d'un atome de plomb est donnée par la relation :
. La masse d'un atome de plomb est donc bien d'environ . [1]
6. Le nombre d'atomes de plomb contenus dans une bille de plomb est d'environ .
En effet :
. [1]
Diamant d'indice de réfraction n
Surface de séparation entre le
diamant et l'air
Rayon incident
limite
Rayon réfracté limite
iC
i2

Page n°4 Contrôle n°4
Masse d'un atome de plomb
Nombre d'atomes de plomb
1
N
7. L'ordre de grandeur du rayon de l'atome de plomb est : . Le volume de l'atome de plomb est donc de : . En effet :
[1]
8. D'après la définition de la masse volumique du plomb, on a :
. La masse volumique du
plomb est donc bien d'environ 102 g.cm3. La valeur précise est de 113,5 g.cm-3 [1]
9. La quantité de plomb déversée serait de 5×101 t. En effet : . [1]
Extrait de la bande dessinée Lefranc Page n°13
CERN : laboratoire européen de physique des particules (initialement
Voir le site : http://public.web.cern.ch/public/welcome-fr.html
Bilan du contrôle n°4
Moyenne (sur 25) :
14,0
Note minimale :
1
Note maximale :
24,5
Nombre de notes strictement inférieures à 12,5 (sur 35) :
14
1
/
4
100%