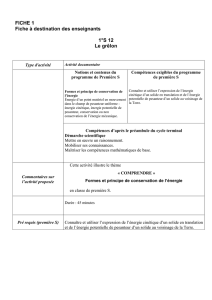
Physique - 2005 - Concours Interne TSE

1
METEO-FRANCE
ECOLE NATIONALE DE LA METEOROLOGIE
CONCOURS INTERNE ET EMPLOIS RESERVES 2005
DE TECHNICIEN SUPERIEUR LA METEOROLOGIE
FILIERE EXPLOITATION
-:-:-:-:-:-
EPREUVE DE PHYSIQUE
Durée : 3 heures Coefficient : 4
-:-:-:-:-:-:-
La clarté des explications et le soin apporté à la présentation seront pris en compte dans
l’évaluation des copies. ______________
Exercice n°1 La scintigraphie
Données susceptibles d’être utilisées
1u=1.66.10-27kg 1u correspond à une énergie de 935MeV 1eV=1,6.10-19J c=3.108m.s-1
masse du noyau de l'iode 123: 122,87652u masse du noyau d'iode 131: 130,87705u
masse du noyau de xénon 131: 130,87545u masse du proton:1,00728u
masse du neutron:1,00866u masse de l'électron: 5,4858.10-4u
Numéro atomique du tellure Te: Z=52 de l'iode I: Z=53 du xénon Xe: Z=54 du césium Cs: Z=55
L'image scintigraphique utilise des traceurs et des marqueurs. Un traceur est une substance qui peut se localiser
de façon sélective au niveau d'une structure particulière de l'organisme. Un marqueur est un radionucléïde qui se
prête aisément à une détection externe. Il émet des rayonnements γ qui sont détectés à l'extérieur de l'organisme
à l'aide d'une gamma-caméra.
L'association d'un traceur et d'un marqueur permet, grâce au marqueur, de suivre l'évolution du traceur dans
l'organisme. Pour réaliser des scintigraphies thyroïdiennes, l'iode radioactif est le traceur physiologique de
référence, il sert à la fois de traceur et de marqueur. On utilise pour cela soit l'iode 131 soit l'iode 123
1) Généralités
a) Donner la structure des noyaux des deux isotopes de l'iode.
b) L'iode 123 est produit par réaction nucléaire entre les deutons 11H de haute énergie et du tellure 12252Te.
Ecrire l'équation correspondant à la réaction nucléaire. Préciser les lois de conservation utilisées et donner la
nature de la particule qui accompagne la formation de l'iode 123.
c) Quelle doit être la caractéristique commune aux deux isotopes de l'iode pour qu'ils puissent être utilisés
comme marqueur?
d) Calculer l'énergie de liaison par nucléon pour chacun des isotopes.
2) Utilisation de l'iode 131 émetteur (β- , γ) de demi-vie t1/2 =8 jours.
a) Quels sont les rayonnements émis par l'iode 131 lors de sa désintégration?
b) Ecrire l'équation de sa désintégration.
c) Calculer, en MeV, l'énergie libérée par chaque désintégration.
d) Pour une scintigraphie thyroïdienne, un patient adulte doit ingérer par voie orale une quantité d'iode 131
d'activité Ao. Le délai entre l'administration du traceur et la réalisation des images est de 24h. Quelle est, en
fonction de Ao, l'activité A de l'iode 131 dans le corps au moment où les images sont réalisées?
T.S.V.P.è
INTERNE - E.R. -
T.S.E

2
3) Utilisation de l'iode 123 émetteur γ de demi-vie t1/2 = 13,2h
a) On rappelle que la constante de temps τ d'un corps radioactif est l'inverse de sa constante radioactive.
Calculer τ pour l'iode 123 en heures et en secondes.
b) Pour une scintigraphie thyroïdienne, il faut injecter à un patient adulte une quantité d'iode 123 d'activité
égale à 6,4MBq. Tracer la courbe représentant L'activité en fonction du temps t ( on tracera la courbe sans
calculatrice, on représentera simplement les activités correspondant à t1/2; 2 t1/2; 3t1/2; 4 t1/2; 5t1/2;…)
c) La réalisation des images se fait entre 2 et 4h après administration de l'iode. Déterminer graphiquement
l'activité de l'iode au bout de 4h. Que vaudrait-elle si on réalisait, comme dans le cas de l'iode 131, une image
24h après l'injection?
Exercice n°2: Chute de grêlons
La grêle, précipitation atmosphérique
formée de grêlons, se produit par
temps orageux au printemps ou en été.
Les grêlons, grains d'eau congelée de
5 à 50 mm de diamètre (qui peuvent
parfois être agglomérés en blocs plus
gros), se forment dans les cumulo-
nimbus orageux, lorsque les gouttes
d'eau, entraînées par des courants
ascendants, gèlent en haute altitude.
On a filmé le mouvement de chute
d’un grêlon de masse m depuis
l’instant de sa formation, pris comme
origine des dates, où l’on peut
considérer que sa vitesse, qualifiée de
vitesse initiale, est nulle.
L’exploitation du fichier vidéo obtenu
permet de tracer la courbe donnant
l’évolution temporelle de la vitesse v
du grêlon. Celle-ci a été représentée ci-contre. On a tracé également la tangente à l’origine de la courbe v = f (t).
I – Exploitation de la courbe
1 ) A la précision de la courbe près, pendant quelle durée peut-on assimiler le mouvement de chute du grêlon à
une chute libre ? Justifier votre réponse.
Quelle est la hauteur de chute correspondante ?
Donnée : g = 10 m.s-2.
2 ) Déterminer, d’après la courbe, la valeur de l’accélération initiale du grêlon.
3 ) En justifiant votre réponse, déterminer la valeur du temps caractéristique relatif au mouvement de chute du
grêlon.
4 ) Déterminer la valeur de la vitesse limite vL du mouvement de chute du grêlon.
II – Choix d’un modèle pour le mouvement de chute du grêlon
1 ) Premier modèle : chute libre
Le grêlon s’est formé en un point O situé à une altitude de 8,0 km du sol. On cherche à savoir si un modèle de
chute libre est adapté.
Dans ce modèle, quelle est la seule force extérieure appliquée au grêlon de masse m ? En appliquant la
deuxième loi de Newton au grêlon, et en adoptant un repère Oz d’axe vertical orienté vers le bas, déterminer les
expressions v (t) de la valeur de la vitesse du grêlon et z (t) de sa hauteur de chute en fonction du temps. Quelle
serait la valeur de la vitesse du grêlon, dans ce modèle, lors de son arrivée au sol ?
2 ) Second modèle : la valeur de la vitesse du grêlon devant manifestement être inférieure à la valeur
précédente, est-ce dû à la poussée d’Archimède ?
Données : masses volumiques : de la glace ρg = 1,0 x 103 kg.m-3 , de l’air ρa = 1,0 kg.m-3.
Vérifier que la poussée d’Archimède ne peut justifier la valeur de la vitesse réellement observée pour le grêlon.
T.S.V.P.è
0
2,5
5
7,5
10
12,5
15
17,5
20
22,5
25
0 2 4 6 8 t (s)
v (m.s-1)

3
3 ) Troisième modèle : existence d’une force de frottement.
L’étude se fera encore dans le repère Oz, d’origine le point O de formation du grêlon et d’axe muni d’un
vecteur unitaire
u
r
vertical et vers le bas. On envisage une force de frottement s’exerçant sur le grêlon dont
l’expression serait : 2
Fkvu
=−⋅⋅
rr
, v étant la valeur de la vitesse du grêlon et k un coefficient constant ne
dépendant que de la forme du grêlon et du fluide dans lequel intervient la chute (ici l’air).
a ) En utilisant l’analyse dimensionnelle, donner l’unité du coefficient k.
b ) En appliquant la deuxième loi de Newton au grêlon, montrer que l’évolution temporelle de la valeur de sa
vitesse est régie par l’équation différentielle suivante : 2
dvk
vg
dtm
+⋅=
(1).
c ) Cette équation peut être résolue à l’aide de la méthode itérative d’Euler. Indiquer brièvement le principe de
cette méthode. En particulier, en désignant par ∆t le pas d’itération, expliciter les calculs que l’on ferait pour
obtenir v (∆t), valeur de la vitesse à la date ∆t, et v (t + ∆t), valeur de la vitesse à la date t +∆t.
d ) Déduire de l’équation (1) l’expression de la valeur de la vitesse limite vL de chute du grêlon dans l’air.
e ) On assimile le grêlon à une sphère de rayon r = 1,0 cm. L’expression du coefficient k est alors : k =
ax
1
SC
2
⋅ρ⋅⋅
, où S =
2
r
π⋅
est la section du grêlon et Cx = 0,50.
Sachant que le volume d’une sphère vaut
3
4
r
3
⋅π⋅
, calculer la valeur théorique de la vitesse limite vL de chute
du grêlon dans l’air. Comparer celle-ci à la valeur expérimentale obtenue au I – 4 ) et conclure sur la validité du
modèle.
Exercice n°3: Réponse d’une bobine à un échelon de tension
On se propose d’étudier l’établissement du courant au travers d’une bobine, d’inductance L et de résistance r,
lorsque celle-ci est soumise à un échelon de tension. Pour obtenir une indication sur la durée nécessaire à
l’établissement d’un régime permanent, on utilise la grandeur notée t, appelée constante de temps du circuit et
définie par
L
R
τ=
.
I – Détermination expérimentale de la valeur numérique de t à partir de l’étude de la courbe
d’établissement du courant.
On donne : R = R’ + r = 50 O.
Un dispositif (centrale d’acquisition) permet d’enregistrer l’évolution, en
fonction du temps, de l’intensité i du courant traversant le circuit. A la
date t = 0 s, on ferme l’interrupteur K. Cette action déclenche la
réalisation des mesures. On obtient la courbe de la figure n° 1 ci-
dessous.
1 ) Soit I l’intensité du courant électrique qui traverse le circuit, en
régime permanent. Etablir l’expression littérale de I à partir des
caractéristiques du circuit. Déterminer sa valeur numérique.
2 ) On admet que l’intensité du courant atteint 63 % de sa valeur
maximale I au bout d’un temps t. Déterminer la valeur de t, constante de
temps du circuit, à partir de la figure n° 1.
II – Vérification de l’expression littérale de t
Pour effectuer cette détermination, l’expérience réalisée dans la partie I – est reprise en conservant pour R la
valeur de 50 O, mais en donnant à L différentes valeurs. Les enregistrements effectués permettent d’obtenir le
faisceau de courbes de la figure n° 2 ci-dessous.
1 ) Déterminer, à partir des enregistrements effectués, les valeurs de t correspondant aux différentes valeurs de
L ; compléter le tableau ci-dessous .
L (H) 0,20 0,40 0,60 0,80
t (ms)
2 ) A partir de l’étude expérimentale, établir par la méthode de votre choix, la relation entre t et L.
3 ) En déduire la valeur expérimentale de R. Est-elle en accord avec les données ?
T.S.V.P.è
K
( L , r )
R’
i
E = 10 V
+

4
III – Détermination de la valeur numérique de t à partir de l’exploitation théorique de la courbe
d’établissement du courant.
1 ) Le circuit étudié est le circuit proposé dans la partie I -. En utilisant la relation d’additivité des tensions dans
un circuit série, donner l’équation différentielle régissant l’établissement du courant dans le circuit.
2 ) Vérifier que
L
R
est homogène à un temps.
3 ) Quelle est la valeur de l’intensité du courant, i (0), à la date t = 0 s ? Comment s’écrit alors l’équation
différentielle donnée précédemment ?
4 ) Déterminer, à la date t = 0 s, l’expression de
di
dt
, que l’on notera
di
dt
(0). En déduire l’équation de la tangente
à la courbe d’établissement du courant à la date t = 0 s, et monter que cette droite passe par i = I à la date t = t.
5 ) Déduire graphiquement de la figure n° 3 ci-dessous, la valeur numérique de t.
T.S.V.P.è

5
L = 0,8 H ; E = 10 V ; R = 50 Ω
0
0,05
0,1
0,15
0,2
0,25
0 20 40 60 80 100 120
t (ms)
i (A)
E = 10 V ; R = 50 Ω
0
0,05
0,1
0,15
0,2
0 20 40 60 80 100 120
t (ms)
i (A)
L = 0,2 H
L = 0,4 H
L = 0,6 H
L = 0,8 H
L = 0,8 H ; E = 10 V ; R = 50 Ω
0
0,05
0,1
0,15
0,2
0,25
0 20 40 60 80 100 120
t (ms)
i (A)
Figure n° 1
Figure n° 2
Figure n° 3