Evolution de la lithosphère océanique, un moteur de la subduction

DM : Evolution de la lithosphère océanique, un moteur de la subduction
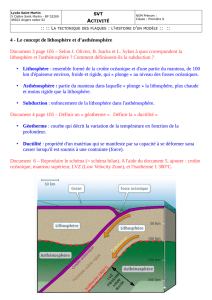
Au cours de son éloignement de l’axe de la dorsale, la lithosphère océanique s’hydrate et se refroidit par
hydrothermalisme. Ce refroidissement se traduit par un abaissement de l’isotherme 1 300°C qui représente la limite
entre la lithosphère et l’asthénosphère : il s’en suit un épaississement progressif de la lithosphère océanique par sa
base, par adjonction d’une semelle de manteau froid et lourd.
1- Calculer l’âge puis l’épaisseur d’une lithosphère océanique (H) située à 800 km de l’axe d’une dorsale ,
dont la demi-vitesse d’écartement est de 8 cm/an.
Sachant que l’épaisseur totale de la lithosphère océanique dépend de son âge selon la formule
H = 9,2 x (âge)1/2,
Soit la colonne de lithosphère océanique d’épaisseur H située à 800 km de l’axe de la dorsale:
constituée d’une croûte océanique d’épaisseur constante hc = 5 km (sans compter les sédiments), et d’une partie sous-
jacente de manteau supérieur d’épaisseur (H – hc).
Nous pouvons donc calculer la
masse de la colonne de lithosphère océanique :
ML= (ρc x hc x S) + ρML x (H – hc) x S avec
ρc : masse volumique de la croûte océanique = 2,85 x 103 kg/m3
ρm: masse volumique du manteau lithosphérique = 3,3 x 103 kg/m3
hc : épaisseur de la croute océanique= 5000 m
S : surface de la colonne étudiée = 1 m2
La masse de la colonne d’asthénosphère sous-jacente, ayant la même surface et la même hauteur H que la colonne
lithosphérique est égale à : MA= ρA x H avec ρA: masse volumique de asthenosphere = 3,25 x 10 3Kg/m3
2- Calculer alors la masse de la colonne de lithosphère océanique en kg et tonnes.
3- Comparer cette masse à celle d’une colonne d’asthénosphère sous jacente de même épaisseur et de
même surface.
4- Calculer la densité de cette colonne de lithosphère océanique (= masse trouvée divisée par le volume de
la colonne)
*Masse volumique ρ = m/V en kg/m³
*Densité d = masse d'un volume V de liquide ou de
solide / masse du même volume V d'eau

Il est possible de réitérer ces calculs à différents niveaux de la croûte océanique :
Distance à l’axe de la
dorsale (en km)
160
800
1200
2000
2400
3200
4800
6400
8000
Age de la lithosphère
(Ma)
2
15
25
30
40
60
80
100
Epaisseur de la croûte
océanique (km)
Epaisseur du manteau
lithosphérique (km)
8
31
41
45
53
66
77
87
Masse d’une colonne de
lithosphère océanique
d’une surface de 1 m2
(en 103 tonnes)
40.7
116.6
149.5
162.8
189.2
232.1
268.4
301.4
Masse d’une colonne
d’asthénosphère de
même surface et de
même épaisseur
(en 103 tonnes)
42.3
117
142.5
162.5
188.5
230.7
266.5
299
Densité de la
lithosphère océanique.
3,13
3,24
3,25
3,26
3,26
3,27
3,27
3,28
Densité de
l’asthénosphère
3,25
3,25
3,25
3,25
3,25
3,25
3,25
3,25
3,25
5- Compléter le tableau à l’aide de l’ensemble des données.
6- Construire un graphique représentant l’évolution de la densité de la lithosphère océanique en fonction de
son âge. Sur ce même graphique, tracer l’évolution de la densité de l’asthénosphère.
7- A partir de quel âge la plaque océanique peut-elle théoriquement plonger ? Expliquer pourquoi elle
plonge en fait beaucoup plus tard.
8- Expliquer pourquoi la plaque océanique subit une traction exercée par la lithosphère océanique
plongeante.

Correction DM : Evolution de la lithosphère océanique, un moteur de la subduction
1) Age de LO située à 800 km sachant que dorsale fonctionne à v= 8 cm/an = 8.10-5 km/an
(âge) = 800/8.10-5= 10 106 ans= 10 Ma.
Epaisseur H = 9,2 x( âge) ½= 29 km
2) ML= ( 2,85.10 3 x 5000 x 1 ) + 3,3.103 x ( 29000-5000) x1 = 93,4 107 kg = 93,45 103 tonnes.
3) Colonne d’asthénosphère : MA= 3,25 103x 29000 = 94,2 103 tonnes. MA > ML
4) Densité de LO=> d= ML/Volume VL= 29000 m3 donc densité = 93,45 103/29000 donc d= 3,22
5) Tableau :
Distance à l’axe de la dorsale (en km)
800
Age de la lithosphère (Ma)
10
Epaisseur de la croûte océanique (km)
5 CONSTANTE
Epaisseur du manteau lithosphérique (km)
29
Masse d’une colonne de lithosphère océanique
d’une surface de 1 m2 (en 103 tonnes)
93,5
Masse d’une colonne d’asthénosphère de même
surface et de même épaisseur
(en 103 tonnes)
94,3
Densité de la lithosphère océanique.
3,22
Densité de l’asthénosphère
3,25
8) La plaque océanique subit une traction car elle est le siège de transformations métamorphiques qui
induisent une augmentation de densité : d (éclogite) > d (métagabbros à glaucophane).
BILAN : Ce qui fait plonger une plaque lithosphérique ….
6) graphique : y=f(x) donc
Ordonnées : densité /abscisses : âge
7) A partir de 27 Ma, la plaque océanique
peut théoriquement plonger car sa
densité devient supérieure a celle de
l’asthénosphère sous jacente, mais
l’asthénosphère exerce une résistance
mécanique qui s’oppose à l’enfoncement
retardant ainsi la subduction.
De plus la cohésion de la plaque lui
permet de se déplacer sur
l’asthénosphère sans plonger.
La LO est constituée de croute : moins dense que l’asthénosphère, et de manteau refroidi : plus
dense que l’asthénosphère donc la LO est une plaque constituée d’un lest (le manteau refroidi )
surmonté d’un flotteur ( la croute). Ce flotteur garde une épaisseur constante tout au long de sa
dérive, mais pas le lest : plus la LO s’éloigne de la dorsale, plus le lest s’épaissit et s’alourdit. Au
bout d’un certain temps, le poids du lest devient théoriquement suffisant pour amorcer la
subduction, malgré le flotteur.
Ce début d’enfoncement est souvent différé de plusieurs millions d’années car la flexion de la LO,
sa fracturation et la résistance de l’asthénosphère exercent une résistance mécanique à
l’enfoncement.
Mais, si à la faveur de mouvements tectoniques, un mouvement de compression survient et
désolidarise la plaque dense de ses flotteurs, alors l’équilibre est rompu : la LO plonge dans
l’Asthénosphère.
Ainsi, une fois la subduction amorcée, l’augmentation de la pression induit des transformations
métamorphiques permettant l’augmentation de la densité (gabbros : d=2,9 se transforment en
schistes bleus d= 3,1 puis en éclogite d= 3,5). Dès que la LO s’est enfoncée, elle tracte le reste
de la plaque : ce qui entretien la subduction.