Pratique des GABARITS Nouveaux programmes de 6ème – Février

Pratique des gabarits pour les angles – Nouveaux programmes de 6
ème
– Février 2005 – page 1
Pratique des GABARITS
Nouveaux programmes de 6
ème
– Février 2005
 Ce qui est dit dans les nouveaux programmes
          !   
 "                         
 "                               
     #                     
                        $
%  
         "                   &      
  '        (        
  '                   %                    )     &   

Pratique des gabarits pour les angles – Nouveaux programmes de 6
ème
– Février 2005 – page 2
 Une possible introduction aux gabarits
F ABRICATION
Par pliage d'un carré et d'un triangle équilatéral, on
obtient un demi-carré et un demi-triangle équilatéral, qui
sont les deux modèles de nos équerres.
On peut y repérer 4 angles (mot connu) que l'on découpe.
Des carrés et des triangles de taille différentes permettront
de remarquer, par superposition, que cela ne dépend pas
de la longueur des côtés.
C LASSEMENT
Classement des 4 angles par superposition
angle 1 > angle 3 > angle 2 > angle 4
C ODAGE
angle 1 est connu comme étant l'angle droit  angle 1 = D
angle 3 est le plus grand des trois autres  angle 3 = G
angle 4 est le plus petit des trois autres  angle 4 = P
angle 2 est moyen entre G et P  angle 2 = M
R ELATIONS
D = M + M
= G + P
= P + P + P
G = D – P
= P + P
M = D – M
P = G – P
= D – G
M ESURES EN DEGRÉ
L'angle droit D est composé de 90 petits angles comme celui-ci :
Cet angle sert d'unité : sa mesure est appelée un degré.
On dira donc que l'angle D mesure 90 degrés (on note 90°).
M est la moitié de D. Donc sa mesure est 90° : 2 = 45°.
P est le tiers de D. Donc sa mesure est 90° : 3 = 30°.
G est le double de P. Donc sa mesure est 30° × 2 = 60°.
Vérifier les autres cases du tableau.

Pratique des gabarits pour les angles – Nouveaux programmes de 6
ème
– Février 2005 – page 3
1
ère
UTILISATION : RECONNAISSANCE DES 4 ANGLES CONNUS
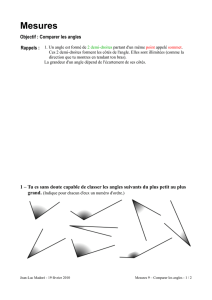
Parmi les angles suivants, reconnais les angles de 90°, de 60°, de 45° et de 30° :
2
ème
UTILISATION : CONSTRUCTION DE NOUVEAUX ANGLES
a) Construction au crayon d'angles de 90°, 60°, 45° et 30° par utilisation des gabarits.
b) Constructions d'angles de 120°, 135°, 150°, 180° par juxtaposition de plusieurs gabarits.
c) Constructions d'un angle de 15° avec les gabarits de 60° et 45°, ou 45° et 30°.
15° pourra devenir un nouveau gabarit.
d) Constructions d'angles de 75°, 105°, ...
3
ème
UTILISATION : MESURES D ' ANGLES COMBINAISONS LINÉAIRES DES ANGLES CONNUS
Inversement à la 2
ème
utilisation, on fait mesurer des angles comme 165° qui est somme de 90°, 60° et 15°.
4
ème
UTILISATION : ÉVALUATION D ' ANGLES
Parmi les angles suivants, sans placer tes gabarits sur la feuille, reconnais ceux dont la mesure est manifestement
fausse :
5
ème
UTILISATION : MESURE D ' ANGLES DE TRIANGLES
Les triangles ont des angles mesurables avec les gabarits :
- 60°, 60°, 60°
- 90°, 60°, 30°
- 90°, 45°, 45°
- 120°, 30°, 30°
- 120°, 45°, 15°
- 135°, 30°, 15°
etc
6
ème
UTILISATION : CONSTRUCTION DE TRIANGLES
Seule la construction d'un triangle connaissant la longueur de ses trois côté est une compétence exigible du
programme.
Cependant, la construction utilisant un ou deux angles entre dans le cadre préconisé par le programme, si elle se fait
en reproduisant un modèle donné (éventuellement à main levée), en réalisant un agrandissement ou une réduction
(éventuellement déjà amorcée), en suivant une description.
7
ème
UTILISATION : FABRICATION DE CADRES
45°
45°
60°
60°
30°
30°
40°
110°
85°
100°
15°

Pratique des gabarits pour les angles – Nouveaux programmes de 6
ème
– Février 2005 – page 4
 Passage à un instrument plus pratique que les gabarits
8
ème
UTILISATION DES GABARITS : PARTAGE DE DISQUES
Partages en 4, en 6, en 8, en 12, en 24 (éventuellement en liaison avec les fractions).
Pour le partage en 6 par exemple, il faut avoir les six gabarits de 60° pour pouvoir les disposer.
Le partage peut ensuite se faire avec un seul gabarit que l'on reporte plusieurs fois.
On peut alors proposer un outil permettant d'aller plus vite :
La fabrication de l'outil permettant de partager en 12, gradué de 30° en 30°,
s'impose d'elle-même :
Il est facile ensuite d'amener à graduer de 10° en 10°,
ce qui constitue une première ébauche du rapporteur :
L'essentiel des exercices de mesure et de construction vus dans le va pouvoir être généralisé à des angles multiples
de 10°.
On remarquera que l'outil est exempt de nombres.
Les angles étudiés étant essentiellement inférieurs à 180°,
on pourra rapidement n'utiliser que la moitié :
 Passage au rapporteur
L'angle de 72° pour partager en 5 par exemple nécessitera le passage à un outil gradué de 1° en 1°.
Si l'idéal serait de continuer avec un instrument sans nombre, il paraît plus difficile à fabriquer.
On pourra alors introduire le rapporteur vendu en commerce.
Le temps passé à utiliser les gabarits doit être suffisamment long pour permettre aux élèves de bien appréhender la
notion d'angle et sa mesure.
On n'hésitera pas à leur consacrer la moitié du temps alloué aux angles, voire plus si besoin.
La compréhension globale de la notion d'angle reste l'objectif prioritaire.
L'utilisation du rapporteur ne lui apportant rien, elle pourra être repoussée à la fin d'année.