DS n°5 - No Math Error à Mourenx

Nom :
Classe : 2nde
Devoir surveillé n°5
le 28/03/2017
Note :
… / 20
Avis de
l’élève
Avis du
professeur
Je sais : Oui Non Oui Non
Exercice 1
Compléter un programme de calcul.
Encadrer le carré d'un nombre.
Exercice 2
Répondre à des questions concrètes en utilisant des savoirs faire mathématiques.
Exercice 3
Justifier la forme canonique d'une fonction polynôme du 2nd degré.
Déterminer un paramètre / Calculer / Résoudre.
Dresser le tableau de signes d'une fonctions polynôme du 2nd degré.
Déterminer les points d'intersection d'une parabole avec les axes d'un repère.
Exercice 4
Etudier les variations d'une fonction polynôme du 2nd degré / Déterminer son extremum.
Utiliser la calculatrice.
Appliquer l'algorithme de dichotomie.
Résoudre une équation du 2nd degré à partir de la forme canonique.
Exercice 1 : Décomposition et ordre. … / 4
L'objectif de cet exercice est de mettre en place un processus, à partir d'un encadrement de , pour encadrer :
=
1. Compléter le programme de calcul suivant :
………
soustraire 1 ………… ……………
2. Compléter les encadrements successifs qui découlent de ce programme de calcul lorsque 1 ≤ ≤ 3 :
1 ≤ ≤ 3 ⇒ … ≤ ≤ …
Or, des nombres ……………… sont rangés dans le même ordre que leurs carrés.
On en déduit : … ≤ ………… ≤ … ⇒ … ≤ ≤ …
3. Faire de même lorsque - 2 ≤ ≤ 1 :
4. Lorsque 0 ≤ ≤ 3, Tom a écrit le raisonnement suivant :
0 ≤ ≤ 3 ⇒ - 1 ≤ ≤ 2 ⇒ 1 ≤ ≤ 4 ⇒ 3 ≤ ≤ 6
En affichant sur votre calculatrice la parabole représentative de la fonction , pensez vous que le
résultat final de Tom soit exact ? Justifier. S'il vous semble faux, corriger le raisonnement de Tom.
Exercice 2 : Un peu de rugby. … / 3
Le week-end dernier, Lilian a essayé de transformer un essai.
La trajectoire du ballon est modélisée par la fonction définie par :
= - + +
où désigne la distance horizontale parcourue par le ballon de rugby,
en mètres, et est la hauteur correspondante, en mètres.
Un logiciel de calcul formel a permis d'obtenir les résultats ci-contre :
1. La fonction est définie sur un intervalle de la forme [0 ; ] où
désigne la distance horizontale parcourue par le ballon avant
de retomber au sol. Déterminer ce réel .
2. Déterminer la hauteur maximale atteinte par le ballon et la distance horizontale alors parcourue.
3. Sachant que le tir de Lilian était cadré, que les poteaux étaient situés à une distance horizontale de 14 m
et à la hauteur de 3,4 m, l'essai a-t-il été transformé ? (Le ballon est-il passé au dessus des poteaux ?)
f(x)
(x¡1)
2
+ 2
x
x
(x¡1)
2
(x¡1)
2
+ 2
x
x
x
f
®
x
®
®
h
h(x)
h(x)
(x¡1)
2
+ 2
x
x¡1
x
x¡1
(x¡1)
2
(x¡1)
2
+ 2
h
x
2
x
1
4
31
8
63
64

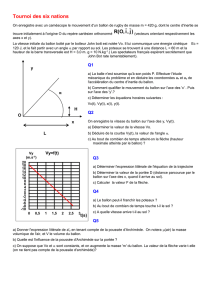
Exercice 3 : On se place dans le repère orthonormé (O ; I , J). … / 6
est la fonction définie sur R par la parabole p tracée ci-contre.
1. a) Justifier graphiquement que, pour tout réel , on peut
définir par une formule de la forme :
=
où est un réel négatif.
b) Le point A ( - 1 ; 0 ) appartient à p.
En déduire le calcul de .
2. On admet que la fonction peut être définie sur R par :
= - + +
a) Justifier que pour tout réel , on a :
=
b) Dresser et justifier le tableau de signe de .
3. On note B le second point d'intersection de p avec l'axe
des abscisses et C celui avec l'axe des ordonnées.
Déterminer les coordonnées de B et C.
Exercice 4 : est la fonction définie sur R par : … / 7
=
1. a) Etudier les variations de et justifier que atteint un extremum, à préciser.
b) En déduire la forme canonique de .
2. On admet que l'équation = 0 admet deux solutions opposées. On note la solution positive.
a) En utilisant le menu graphe de la calculatrice, donner un encadrement de à l'unité près.
b) On rappelle ci-dessous l'algorithme de dichotomie :
Compléter le tableau suivant en appliquant cet algorithme pas à pas avec = 1, = 2 et = 3.
Signe de Test Réaffectations
× < 0 ?
Quel encadrement de obtient-on ?
3. Le nombre recherché est appelé le nombre d'or.
En résolvant l'équation = 0 à partir de la forme canonique, déterminer la valeur exacte de .
x
f
a(x¡2)
2
+ 6
f(x)
a
p
a
f(x)
2
3
x
2
8
3
x
10
3
f
x
f(x)
2
3
f
f(x)
f
(x+ 1)(5 ¡x)
f(x)
f
f(x)
x
2
¡x¡1
f(x)
Á
Á
a
b
N
i
a
m
b
f(a)
f(m)
f(a)
f(m)
a
b
Á
Á
f(x)
Á
f

Correction du DS n°5
Exercice 1 : Décomposition et ordre.
L'objectif de cet exercice est de mettre en place un processus, à partir d'un encadrement de , pour encadrer :
=
1. Compléter le programme de calcul suivant :
soustraire 1 mettre au carré ajouter 2
2. Compléter les encadrements successifs qui découlent de ce programme de calcul lorsque 1 ≤ ≤ 3 :
1 ≤ ≤ 3 ⇒ 0 ≤ ≤ 2
Or, des nombres positifs sont rangés dans le même ordre que leurs carrés.
On en déduit : 0 ≤ ≤ 4 ⇒ 2 ≤ ≤ 6
3. Faire de même lorsque - 2 ≤ ≤ 1 :
- 2 ≤ ≤ 1 ⇒ - 3 ≤ ≤ 0
Or, des nombres négatifs sont rangés dans l'ordre contraire de leurs carrés.
On en déduit : 0 ≤ ≤ 9 ⇒ 2 ≤ ≤ 11
4. Lorsque 0 ≤ ≤ 3, Tom a écrit le raisonnement suivant :
0 ≤ ≤ 3 ⇒ - 1 ≤ ≤ 2 ⇒ 1 ≤ ≤ 4 ⇒ 3 ≤ ≤ 6
En affichant sur votre calculatrice la parabole représentative de la fonction , pensez vous que le
résultat final de Tom soit exact ? Justifier. S'il vous semble faux, corriger le raisonnement de Tom.
Le résultat est faux car le minimum de sur [0 ; 3] est 2 (atteint quand = 1) et 2 ∉ [3 ; 6].
Correction du raisonnement de Tom :
0 ≤ ≤ 3 ⇒ - 1 ≤ ≤ 2 ⇒ 0 ≤ ≤ 4 ⇒ 2 ≤ ≤ 6
x
f(x)
(x¡1)
2
+ 2
x
(x¡1)
2
(x¡1)
2
+ 2
x
x
x¡1
(x¡1)
2
+ 2
x
x
x
x¡1
(x¡1)
2
(x¡1)
2
+ 2
f
x¡1
(x¡1)
2
x¡1
(x¡1)
2
(x¡1)
2
+ 2
x
f
x
x¡1
(x¡1)
2
(x¡1)
2
+ 2
x

Exercice 2 : Un peu de rugby.
Le week-end dernier, Lilian a essayé de transformer un essai.
La trajectoire du ballon est modélisée par la fonction définie par :
= - + +
où désigne la distance horizontale parcourue par le ballon de rugby,
en mètres, et est la hauteur correspondante, en mètres.
Un logiciel de calcul formel a permis d'obtenir les résultats ci-contre :
1. La fonction est définie sur un intervalle de la forme [0 ; ] où
désigne la distance horizontale parcourue par le ballon avant de
retomber au sol. Déterminer ce réel .
Remarque 1 : Dans cette question, n'a rien à voir avec l'abscisse du
sommet de la parabole qui décrit la trajectoire du ballon.
Chercher la valeur de revient à chercher la distance horizontale qui
correspond à l'impact du ballon au sol. De plus, la trajectoire du ballon
n'est définie par que si ≥ 0 et ≥ 0.
On utilise la forme factorisée : = -
> 0 ⇔ > ⇔ >
64 > 0 donc > 0 ⇔ > 0 ⇔ > - ⇔ >
On en déduit le tableau de signes suivant :
- ∞ 0 + ∞
- 1 – – – –
– – – +
– + + +
– + + –
Puisque n'est définie que si ≥ 0 et ≥ 0 alors la fonction est
définie sur [0 ; ], c'est-à-dire [0 ; ].
Remarque 2 : On pourrait en déduire que le ballon touchera le sol à une
distance horizontale de 15,75 m.
Modélisation de la situation :
2. Déterminer la hauteur maximale atteinte par le ballon et la distance horizontale alors parcourue.
= < 0 confirme que la fonction atteint un maximum.
En utilisant la forme canonique : = , on en déduit que la hauteur maximale
atteinte par le ballon est de 16 m. Elle est atteinte pour une distance horizontale de = 7,75 m.
3. Sachant que le tir de Lilian était cadré, que les poteaux étaient situés à une distance horizontale de 14 m
et à la hauteur de 3,4 m, l'essai a-t-il été transformé ? (Le ballon est-il passé au dessus des poteaux ?)
La question est de savoir si pour une distance parcourue horizontalement de 14 m le ballon sera au
dessus des poteaux ou non, sachant que les poteaux sont à une hauteur de 3,4 m.
= - + + ≈ - 49 + 54,25 + 0,98 ≈ 6,23 > 3,4
On en déduit que le ballon est passé au dessus des poteaux et que Lilian a transformé l'essai.
h
h(x)
1
4
x
2
31
8
x
63
64
x
h(x)
h
®
®
®
h(x)
h(x)
h(x)
(4x¡63)
4x+1
64
4x¡63
4x
63
x
63
4
4x+1
64
4x
x
4x+ 1
1
-1
4
x
4x¡63
4x+1
64
h(x)
x
-1
4
63
4
O
O
O
O
h(x)
x
h(x)
63
4
h
15,75
®
®
h(x)
-1
4
(x¡
31
4
)
2
+ 16
a
-1
4
h
31
4
14
1
4
31
8
63
64
h(14)
£14
2
£14

Exercice 3 : On se place dans le repère orthonormé (O ; I , J).
est la fonction définie sur R par la parabole p tracée ci-contre.
1. a) Justifier graphiquement que, pour tout réel , on peut
définir par une formule de la forme :
=
où est un réel négatif.
Puisque p est une parabole ouverte vers le bas, la
fonction est une fonction du 2nd degré définie par une
formule de la forme = avec < 0.
où ( ; ) sont les coordonnées du sommet S de p.
Graphiquement : = 2 et = 6.
Donc : ∀ ∈ R, =
b) Le point A ( - 1 ; 0 ) appartient à p.
En déduire le calcul de .
= = =
A ( - 1 ; 0 ) ∈ p ⇔ = 0 ⇔ = 0
= -
= =
2. On admet que la fonction peut être définie sur R par : = - + +
a) Justifier que pour tout réel , on a : =
∀ ∈ R, = = = - + + =
b) Dresser et justifier le tableau de signe de .
On utilise la forme factorisée : =
> 0 donc le signe de ne dépend que des signes de et de .
> 0 ⇔ > - 1
> 0 ⇔ > ⇔ <
On en déduit le tableau de signes de :
- ∞ - 1 5 + ∞
– + +
+ + –
– + –
3. On note B le second point d'intersection de p avec l'axe des abscisses et C celui avec l'axe des
ordonnées. Déterminer les coordonnées de B et C.
D'après le tableau des signes de , on sait que : = 0 ⇔ = - 1 ou =
On en déduit que les points d'intersection de p avec l'axe des abscisses sont A ( - 1 ; 0 ) et B ( 5 ; 0 ).
De plus : = - + + =
On en déduit que le point d'intersection de p avec l'axe des ordonnées est C ( 0 ; ).
f
x
f
f(x)
a(x¡2)
2
+ 6
a
a
p
f(x)
a
a(x¡®)
2
+¯
®
¯
®
¯
f(x)
a(x¡2)
2
+ 6
x
f
S
×
f(-1)
a(-1 ¡2)
2
+ 6
9a+ 6
a(-3)
2
+ 6
f(-1)
9a+ 6
9a
6
a
-6
9
-2
3
f
f(x)
2
3
x
2
8
3
x
10
3
x
f(x)
2
3
(x+ 1)(5 ¡x)
f(x)
2
3
(x+ 1)(5 ¡x)
2
3
(5x¡x
2
+ 5 ¡x)
2
3
(-x
2
+ 4x+ 5)
2
3
x
2
8
3
x
10
3
f(x)
x
O
O
O
x
x
x+ 1
x
5
5
x+ 1
5¡x
5¡x
f(x)
f(x)
2
3
(x+ 1)(5 ¡x)
O
f(x)
2
3
f(x)
x+ 1
5¡x
f(x)
f(x)
x
x
5
2
3
8
3
10
3
f(0)
£0
2
£0
10
3
10
3
B
×
C
×
x