Les quadrilatères

[Les quadrilatères \
Table des matières
I Trapèze 1
II Parallélogramme 2
III Losange 2
IV Rectangle 3
V Carré 4

Cours Les quadrilatères
I Trapèze
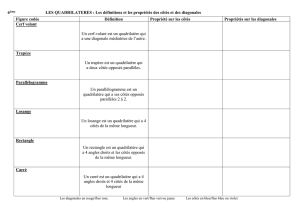
Un trapèze est un quadrilatère qui a deux côtés parallèles.
Les côtés parallèles s’appellent les bases du trapèze.
Définition
A
B
C
DABCD est un trapèze
[AB] et [CD] sont les bases
Un trapèze rectangle est un trapèze qui a un angle droit .
Définition
ABCD est un trapèze rectangle
A
B
D
C
Un trapèze isocèle est un trapèze qui a un axe de symétrie.
Définition
ABCD est un trapèze isocèle
A
D
C
B
http://mathparadise.pagesperso-orange.fr Page 1/4

Cours Les quadrilatères
II Parallélogramme
Un parallélogramme est un quadrilatère qui a ses côtés parallèles deux à deux.
Définition
AB
C
D
(AB) Ë(CD)
(AD) Ë(BC)
P1Les diagonales d’un parallélogramme se coupent en leur milieu.
P2Un parallélogramme a ses côtés opposés de la même longueur.
P3Un parallélogramme a ses angles opposés égaux.
Propriétés
A
D
C
B
O
Si ABCD est un parallélogramme alors
– (AB) Ë(CD) et (AD) Ë(BC) ;
– AB=CD et AD=BC ;
– O est le milieu de [AC] et de [BD].
P’1Si les diagonales d’un quadrilatère se coupent en leur milieu, alors c’est un parallélogramme.
P’2Si un quadrilatère non croisé a ses côtés opposés de la même longueur alors c’est un parallélo-
gramme.
P’3Si un quadrilatère a deux côtés parallèles et de la même longueur alors c’est un parallélo-
gramme.
P’4Si les angles opposés d’un quadrilatère sont égaux alors c’est un parallèlogramme.
Propriétés caractéristiques
http://mathparadise.pagesperso-orange.fr Page 2/4

Cours Les quadrilatères
III Losange
Un losange est un quadrilatère dont les quatre côtés ont la même longueur.
Définition
P1Un losange a ses côtés parallèles deux à deux, c’est donc un parallélogramme particulier.
P2Un losange a ses diagonales perpendiculaires.
Propriétés
A
D
C
B
O
Si ABCD est un losange alors
– AB=BC=CD=DA ;
– (AB)/ /(CD) et (AD)/ /(BC) ;
– O est le milieu de [AC] et de [BD] :
– (AC) perpendiculaire à (BD)
P′
1Si les diagonales d’un parallélogramme sont perpendiculaires, alors c’est un losange.
P′
2Si un parallélogramme a deux côtés consécutifs de même longueur alors c’est un losange.
Propriétés caractéristiques
IV Rectangle
Un rectangle est un quadrilatère qui a quatre angles droits
Définition
P1Un rectangle a ses côtés parallèles deux à deux, c’est donc un parallélogramme particulier.
P2Un rectangle a ses diagonales de même longueur.
Propriétés
http://mathparadise.pagesperso-orange.fr Page 3/4

Cours Les quadrilatères
A
B
C
DO
Si ABCD est un rectangle alors
– (AB) Ë(CD) et (AD) Ë(BC) ;
– AB=CD et AD=BC ;
– O est le milieu de [AC] et de [BD] ;
– (AB)⊥(BC), (BC)⊥(CD), (CD)⊥(DA) et
(DA)⊥(AB) ;
– OA=OB=OC=OD.
P′
1Si un quadrilatère a trois angles droits alors c’est un rectangle.
P′
2Si un parallélogramme a deux côtés consécutifs perpendiculaires alors c’est un rectangle.
P′
3Si les diagonales d’un parallélogramme sont de même longueur, alors c’est un rectangle.
Propriétés caractéristiques
V Carré
Un carré est un quadrilatère qui à quatre angles droits et quatre côtés de même longueur.
Définition
Un carré a toutes les propriétés d’un rectangle et celles d’un losange.
Propriétés
B
C
D
A
O
Si ABCD est un carré alors
– (AB) Ë(CD) et (AD) Ë(BC) ;
– AB = CD = AD = BC ;
– O est le milieu de [AC] et de [BD] ;
– (AB)⊥(BC), (BC)⊥(CD), (CD)⊥(DA) et
(DA)⊥(AB) ;
– OA = OB = OC = OD.
Pour prouver qu’un quadrilatère est un carré il faut prouver que c’est un losange et un rectangle.
Propriétés caractéristiques
http://mathparadise.pagesperso-orange.fr Page 4/4