1 Un objet aléatoire de base : le dé 2 Fluctuation d`échantillonnage

BTS ACSE/GPN/TV Travaux dirigés
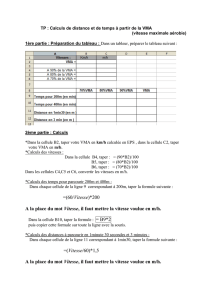
Dans le monde des statistiques, il est bien évident qu’on ne fait plus aucun calcul à la main. Si nous le
faisons en cours de mathématiques, c’est pour mieux comprendre ce que font les divers logiciels et pour
connaître les pièges de ces notions.
L’un des logiciels utiles et surtout gratuit (argument important pour nous étudiants et professeurs) est le
logiciel (http://www.r-project.org/). Bien qu’en anglais, il reste accessible mais néanmoins extré-
mement puissant.
Commençons son exploration par les bases.
1 Un objet aléatoire de base : le dé
1. Démarrer le logiciel R (Démarrer/tous les programmes/R/R 2.9.2).
2. Quand on lance un dé non truqué, les résultats possibles sont 1, 2, 3, 4, 5 ou 6.
(a) Précisons au logiciel ce qu’est un dé avec l’instruction : d=1:6
(b) Demandons maintenant ce que contient l’objet d en tapant simplement : d
On dit que d est un objet liste.
3. Pour un logiciel, lancer un dé c’est donc choisir au hasard un nombre dans l’ensemble des résultats
possibles.
(a) C’est aussi un échantillon de taille 1 de l’objet d : sample(d,1)
(b) Avec la flèche vers le haut, rappeler plusieurs fois cette commande. Obtient-on toujours le même
résultat ? Le dé est-il équilibré ?
(c) Lancer le dé 6 fois à l’aide de la seule commande : sample(d,6)
Relancer plusieurs fois cette commande. A-t-on ce que l’on espère ? Qu’est-ce qui semble « louche» ?
(d) Demander l’aide sur cette fonction en tapant : help("sample")
Comment faire pour obtenir 6 lancers du dé ? Peut-on truquer le dé ?
4. Présentons de nombreuses informations :
(a) Lancer 100 fois le dé et ranger les résultats dans la variable s : s=sample(d,100,T)
(b) afficher le contenu de s en tapant simplement : s
Remarque : On aurait pu tout faire en une seule ligne, il suffit de séparer les instructions par un
point-virgule, comme ceci : s=sample(d,100,T) ; s
(c) Les données sont illisibles du fait de leur grand nombre.
Résumons les à l’aide d’un tableau : t=table(s) ; t
Présentons ce tableau à l’aide d’un diagramme en barre : barplot(t)
5. Construisons maintenant une fonction qui fasse toutes les étapes. Nous souhaitons simplement pouvoir
donner le nombre de lancers.
(a) Taper :
f=function(n){d=1:6 ; s=sample(d,n,T) ; t=table(s) ; print(t) ; barplot(t)}
(b) essayer la fonction avec : f(500)
2 Fluctuation d’échantillonnage
1. Taper f(100), puis à nouveau f(100)
Que s’est-il passé ?
Ce phénomène est appelé fluctuation d’échantillonnage 1.
2. Rappeler la commande f(100) plusieurs fois pour observer cette fluctuation.
1. Le changement de hauteur des barres du diagramme indique la fluctuation d’échantillonnage.

Travaux dirigés BTS ACSE/GPN/TV
3. Recommencer et observer la fluctuation d’échantillonnage avec 1000 lancers puis 10000 lancers,
100000 lancers et 1000000 lancers.
Quelle conclusion concernant la fluctuation d’échantillonnage peut-on déduire de ce qui précède ?
4. Quand on lance un dé bien équilibré on a 1 chance sur 6 d’obtenir la face 5 (de même pour les autres
faces). Retrouve-t-on ce résultat ?
5. Application : deviner la composition de l’urne.
Une urne bien cachée dans la mémoire de l’ordinateur contient 470 boules de couleurs. Le but de
l’exercice est de trouver la composition de cette urne.
(a) Ouvrir le fichier « Secrets ».
(b) Que réalise l’instruction suivante : s=sample(urnesecrete,1,T) ; s ?
(c) On étudie des échantillons de taille 10 et on observe les tables et les diagrammes obtenus :
s=sample(urnesecrete,10,T) ; t=table(s) ; t ; barplot(t)
Quelles sont les couleurs des boules contenues dans l’urne ?
(d) En modifiant la taille de l’échantillon, déterminer la composition de l’urne en pourcentage. Com-
menter votre démarche et présenter un diagramme qui justifie votre réponse. En déduire la com-
position de l’urne.
3 Le problème des sondages
Nous savons tout, nous voyons tout ! On imagine une population composée de 1000000 d’individus. La
moitié des individus possèdent une certaine caractéristique qui est codée par le chiffre 1. L’autre moitié est
codée par 0. On effectue des sondages dans cette population et étudie les résultats.
1. On définit la population : population=c(rep(0,500000),rep(1,500000))
2. (a) Un échantillon de 1000 : échantillon=sample(population,1000) ; échantillon
(b) Dans cet échantillon, combien d’individus possèdent la caractéristique étudiée ?
s=sum(échantillon)
(c) Quel pourcentage cela représente-t-il? s*100/1000
(d) En abrégé : s=sum(sample(population,1000))/10 ; s
3. En rappelant cette instruction vous obtiendrez le résultat d’autant de sondages que vous le souhai-
tez. . .chose qu’on ne peut pas se permettre en réalité.
(a) Dans quel intervalle se trouvent les résultats observés ?
(b) Dans la population choisie on sait que 50% des personnes possèdent la caractéristique étudiée.
Quelle est la marge d’erreur induite par le sondage ?
4. Pour affiner cette estimation nous allons faire un grand nombre de sondages, par exemple 500 son-
dages.
(a) L’instruction est la suivante :
L=c() ; for(i in 1:500) L=c(sum(sample(population,1000))/10,L)
(b) Pour analyser les résultats : hist(L,prob=TRUE)
Quelle loi de probabilité peut produire cet histogramme ?
Un indice de plus ? Taper l’instruction : hist(L,prob=TRUE,nclass=20)
Un indice de plus ? Taper l’instruction : lines(density(L,bw=1))
(c) Calculons quelques valeurs caractéristiques :
• Taper l’instruction : mean(L), la moyenne µdes 500 échantillons est :
• Taper l’instruction : sd(L), l’écart type σdes 500 échantillons est :
• Taper l’instruction : length(L[(L>mean(L)-sd(L))&(L<mean(L)+sd(L))])/500,
le pourcentage des 500 échantillons dans l’intervalle [µ−σ;µ+σ]est :

BTS ACSE/GPN/TV Travaux dirigés
• Taper l’instruction : length(L[(L>mean(L)-2*sd(L))&(L<mean(L)+2*sd(L))])/500,
le pourcentage des 500 échantillons dans l’intervalle [µ−2σ;µ+2σ]est :
• Taper l’instruction : length(L[(L>mean(L)-3*sd(L))&(L<mean(L)+3*sd(L))])/500,
le pourcentage des 500 échantillons dans l’intervalle [µ−3σ;µ+3σ]est :
• Taper l’instruction : length(L[(L>mean(L)-2/3*sd(L))&(L<mean(L)+2/3*sd(L))])/500,
le pourcentage des 500 échantillons dans l’intervalle [µ−2
3σ;µ+2 3σ]est :
• Calculer 100 ×Æ0,5(1−0,5)
1000 et le comparer avec σ.
(d) À l’aide du graphique ci-dessous repris du cours et des informations trouvées ci-dessus, quelle
est la loi de la variable aléatoire X où X est la fréquence en pourcentage des individus ayant une
certaine caractéristique dans un échantillon de 500 individus choisis de manière indépendante ?
µ−3σ µ −2σµ−σ
µ−2
3σ
µ
µ+2
3σ
µ+σµ+2σ µ +3σ
1
σp2π
0,5
0,68
0,95
0,997
(e) Taper l’instruction : quantile(L,c(0.025,0.975)). La réponse signifie que 95% des résultats
sont dans l’intervalle affiché.
• Quelle est la valeur de ktelle que Φ(k) = 0,975 ?
• Que vaut µ−1,96σ? Que vaut µ+1,96σ?
• Si la loi de X est la loi N(µ;σ), que vaut P(µ−1, 96σ¶X¶µ+1,96σ)?
• Cela explique-t-il les valeurs trouvées par le logiciel au début de la question ?
5. Application : Nous ne savons rien, nous ne voyons que le résultat d’un seul sondage !
Vous réalisez un sondage sur un échantillon de 1000 personnes parmi la population de Secreteville
(qui comporte 1 million d’habitants).
Vous posez la question suivante : « Pensez-vous que l’étude des statistiques au lycée soit utile ? ».
La réponse « oui » est codée par 1 et la réponse « non » est codée par 0.
Quelle estimation pourriez-vous publier ? Donner par calcul un intervalle dans lequel on trouvera 95%
des estimations.
4 Un premier test statistique : le test du χ2
Le dé que vous lancez est-il vraiment bien équilibré ?
Les résultats que l’on obtient en lançant un dé sont censés suivre la loi uniforme : à chacun des 6 résultats
possibles, on attribue la probabilité 1
6; c’est la symétrie du cube qui nous amène à penser cela.

Travaux dirigés BTS ACSE/GPN/TV
En pratique cependant, on observe une certaine fluctuation des résultats : si on lance le dé 120 fois, il est
rarissime d’obtenir exactement 20 résultats de chaque sorte !
À titre d’exemple, on pourrait obtenir la table suivante :
résultat 1 2 3 4 5 6
Effectifs observés 21 16 22 24 18 19
Effectifs théoriques 20 20 20 20 20 20
Il n’est pas évident, au vu de ces résultats, de déterminer si les différences sont dues à des fluctuations
normales, ou si elles sont dues à un déséquilibre du dé.
4.1 Élaboration d’un test
1. Dans Fichier, Charger l’environnement de travail, choisir d’ouvrir le fichier « adequat.R ».
2. Vous pouvez maintenant faire un grand nombre d’essais, sur un dé de référence parfaitement équilibré :
(a) Tapez n_Lancers(), 120 résultats s’affichent ;
(b) Une simple table des résultats serait plus lisible ; ou bien un tracé en bâtons
Tapez Dé0(), et vous obtiendrez les 2.
(c) En rappelant la ligne précédente avec la touche « flèche vers le haut », vous pouvez effectuer un
grand nombre d’essais. Ceci permet de se faire une première idée des fluctuations possibles sur
un dé bien équilibré.
L’appréciation de ces fluctuations nécessite la prise en compte simultanée de 6 valeurs numé-
riques ;
3. La tâche serait plus facile si on synthétisait ces informations en une seule valeur numérique.
L’idée est de mesurer l’écart entre les effectifs observés et les effectifs théoriques.
(a) tapez observés= Dé0() ; théorique=20
(b) Puis différence = observés - théorique
(c) Puis (différence)ˆ2 qui donne les carrés des valeurs précédentes.
(d) sum(différence) donne toujours 0 ; et donc aucune information.
(e) Par contre sum((différence)ˆ2) n’est nul que si les valeurs théoriques et observées coïncident
(ce qui est rarissime) et croit quand les écarts croissent. Nous prendrons cette valeur comme
indicative de l’écart « théoriques par rapport à observées », et la noterons ECART.
(f) Pour en faciliter les calculs, tapez en une ligne Obs=Dé0() ; E=sum((Obs-20)ˆ2) ; Obs ;
paste(« ECART= »,E)
Puis rappelez cette ligne d’instruction grâce à la touche « flèche vers le haut » autant de fois que
vous le souhaitez.
Vous aurez ainsi une petite idée des valeurs possibles de l’ECART. Notez 20 de ces valeurs.
(g) Pour avoir une idée plus claire des valeurs possibles de ECART, nous allons collecter par simula-
tions un grand nombre de valeurs de ECART.
La fonction N_ECARTS() collecte 1000 valeurs de ECART et renvoie les résultats sous forme d’une
représentation graphique.
Ce graphique, que nous appellerons graphique de référence, montre bien quelles sont les valeurs
typiques auxquelles nous devons nous attendre.
Souvenez vous que ces valeurs constituent une mesure des fluctuations ordinaires d’un dé parfai-
tement équilibré

BTS ACSE/GPN/TV Travaux dirigés
4. Pour aller plus loin il faut décider d’un critère de sélection.
Rangeons les 1000 valeurs de ECART par ordre croissant et notons E0.95 la 950ème valeur , c’est à dire
le 95ième centile de cette série de 1000 valeurs. Dans la simulation de référence , 95% des résultats
sont inférieurs à E0.95.
Un résultat supérieur sera considéré comme excentrique, même si, notez-le bien, il a été obtenu par
le lancer d’un dé bien équilibré, notre dé de référence ! Notez également le caractère arbitraire de ce
choix ; arbitraire mais raisonnable !
la fonction N_Ecarts() recalcule un graphique de référence et y adjoint le nombre E0.95 que nous
appellerons valeur critique ;
On obtient un graphique comme le suivant :
95% des valeurs de ECART sont inferieures à 214
1000 valeurs de ECART, calculées sur 120 lancers
effectifs
0 50 100 150 200 250 300 350
0 100 200 300
Placez les 20 résultats obtenus en 3f sur votre graphique de référence. Combien de valeurs sont infé-
reures à E0.95 ?
4.2 Mise en œuvre du test
Soit à tester un nouveau dé. On décide de l’accepter comme bien équilibré si la valeur de ECART que l’on
obtient suite à 120 lancers est inférieure à E0.95 ; dans le cas contraire , il est écarté .
Vous avez 9 dés à tester.
1. Pour lancer 120 fois le dé numero 7, tapez Dé7() ;
2. Pour calculer la valeur de ECART relative à ce lancer, tapez :
Obs=Dé7() ; E=sum((Obs-20)ˆ2) ; Obs ; paste(« Ecart= »,E)
Puis comparez le résultat à la valeur critique lue sur votre graphique de référence.
3. Pour vous faciliter la tâche, il existe une fonction Test , dont la syntaxe est Test(Dé7,120) qui donne
une table portant sur 120 lancers du dé numéro 7, un graphique et la valeur de l’Ecart correspondant.
4. Quels dés retiendriez-vous ?