TD(TS2) - GSEM - Physique Chimie au lycée par Wahab Diop LSLL

1/2
Groupe Scolaire Edoukou Miezan Année Scolaire : 2013-2014
de Grand – Bassam
P H Y S I Q U E - C H I M I E
Consignes générales :
 Toute calculatrice est autorisée, mais il est formellement interdit de la prêter à son voisin.
 L’usage du Blanco est interdit ;
 Le soin et la rigueur de l’écriture des formules seront pris en compte dans la note finale.
 Rédaction + propriétés de la copie : 1 point
EXERCICE 1 : 8 points
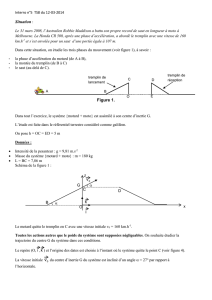
Le 31 mars 2008, l'australien Robbie Maddison a battu son propre record de saut en longueur à moto à Melbourne. La Honda
CR 500, après une accélération, a abordé le tremplin avec une vitesse de 160 km/h et s'est envolée pour un saut d'une portée
égale à 107 m.
Dans cet exercice on étudie les trois phases du mouvement, à savoir :
- la phase d'accélération du motard de A à B
- la montée du tremplin de B à C
- le saut au-delà de C.
Dans tout l'exercice, le système {motard + moto } est assimilé à son centre d'inertie G. l'étude est faîte dans le référentiel
terrestre considéré comme galiléen.
On pose h = OC =ED ; g = 9,81 m s
; masse du système m = 180 kg ; L = BC =7,86 m.
1. La phase d'accélération du motard.
On considère que le motard s'élance, avec une vitesse initiale nulle, sur une piste rectiligne en maintenant une accélération
constante.
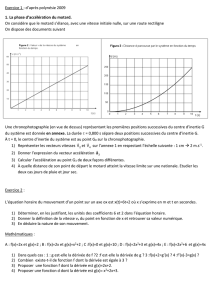
Une chronophotographie (en vue de dessus) représentant, à l’échelle 1cm pour 2 m, les premières positions successives du
centre d'inertie G du système est donnée. La durée  =0,800 s sépare deux positions successives du centre d'inertie G.
A t = 0, le centre d'inertie du système est au point A ( G0 sur la chronophotographie).
1.1 Calculer les valeurs des vecteur-vitesses du centre d'inertie G aux points G
 et G .
1.2 Déterminer la valeur a de l’accélération du motard.
1.3 Calculer la distance AB parcouru par Robbie et son engin s’ils arrivent en B avec la vitesse de 160 km/h..
2. La montée du tremplin.
Le motard aborde le tremplin au point B, avec une vitesse de 160 km/h et maintient cette vitesse jusqu'au point C. Le tremplin
est incliné d'un angle de α =27° par rapport à l'horizontale.
2.1 Quelle est la nature du mouvement du motard sur ce parcours ? Justifier.
2.2 Établir l’équation horaire du mouvement du motard.
2.3 Au bout de combien de temps parcourt-il la distance L ?
3. Le saut.
Le motard quitte le tremplin en C avec une vitesse initiale v
 = 160 km/h.
Toutes les actions autres que le poids sont supposées négligeables. On souhaite étudier la trajectoire du centre d'inertie G du
système dans ces conditions. L'origine des dates est choisie à l'instant où le système quitte le point C
Classe : Tle D
Durée : 2 heures
DEVOIR N° 02
Cours à domicile: 779165576
(C) Wahab Diop 2013-2014
Ce document a été téléchargé sur http://physiquechimie.sharepoint.com
http://physiquechimie.sharepoint.com

2/2
3.1 En appliquant la seconde loi de Newton, établir les équations horaires du mouvement du point G dans le repère
(O,  i ,  k).
3.2 Montrer que l'équation de la trajectoire est : z(x) = – g
v
cos α x
+ x.tanα + L.sinα
3.3 À quelle distance maximale de C doit se trouver le point D pour que "l'atterrissage" se fasse sur le tremplin ?
3.4 Comparer cette valeur à celle donnée dans l'énoncé. Comment peut-on interpréter cet écart ?
EXERCICE 2 : 6 points
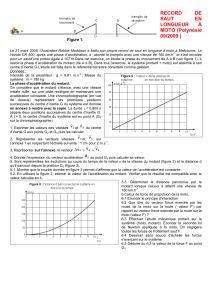
Un électron animé, d’une vitesse  v
 horizontale pénètre dans un champ uniforme 
E au point O à la date t = 0. Il sort du champ à
la date t = 2.10
s au point S, puis produit un impact sur l’écran placé à la distance D de l’extrémité des plaques (voir figure).
La déflexion électrique Y
m est telle que Y m = O’P = 50 mm.
1. Établir l’équation cartésienne de la trajectoire de
l’électron dans le repère (O, x, y).
2. Déterminer la valeur v
 du vecteur-vitesse 
v
 avec
laquelle l’électron pénètre dans le champ  E.
3. Calculer la valeur du champ électrostatique  E en
utilisant l’expression littérale de Y
m.
4. Déterminer la valeur de la tension U
AB établie entre les
plaques A et B.
On donne : d = 5 cm ; l = 10 cm ; D = 50 cm ; m = 9,1.10 
Kg
N.B : On admet que la tangente de la trajectoire au point S passe
par le point I, milieu des plaques.
EXERCICE 3 : 5 points
1. On prépare une solution aqueuse S
 de chlorure de baryum BaCl  de volume V  = 250 cm et de concentration C , en
dissolvant une masse m
 de BaCl  dans l’eau.
1.1 Écrire l’équation bilan de cette dissolution.
1.2 Vérifier que C
1= 4,25.10  mol/L On donne : [Cl  ]  = 8,5.10  mol/L.
1.3 En déduire m
.
2. On prélève un volume V
 = 50 cm de S  qu’on complète avec un volume V e d’eau distillée pour obtenir une solution S
de volume V
S = 200 cm de concentration molaire C S = 1,06.10  mol/L.
Calculer V
e .
3. Dans 25 cm
de S , on verse V  = 75 cm d’une solution S  de soude dans laquelle [OH  ] = 3,5.10  mol/L.
On rappelle que l’expérience se déroule à 25°C et que les ions OH 
réagissent avec les ions Ba pour donner Ba( )
OH
.
3.1 Écrire l’équation bilan de la réaction.
3.2 Déterminer la quantité d’ions OH 
qui restent dans le mélange.
3.3 Calculer le pH du mélange obtenu.
Données : M(Ba) = 137,3 g/mol ; M(Cl) = 35,5 g/mol.
Prof : M. Ané
x
O’
P
I
S
O
B
A
l
v
D
y
Cours à domicile: 779165576
(C) Wahab Diop 2013-2014
Ce document a été téléchargé sur http://physiquechimie.sharepoint.com
http://physiquechimie.sharepoint.com