Exercice n°1 : Centre de masse d`un cylindre et d`un cône

R
h
L M
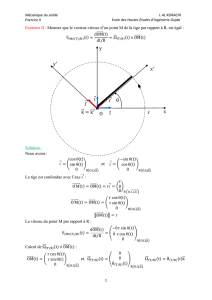
L Oxy ω
O θ ˙ θ=ω(R)
(Ox, Oy)
(R∗)
(R∗)
−→
P
−→
LOM, L, ω
−→
L∗
−→
L∗(R∗)
(S)
m
O
Oz
L
θ
P
P0
−→
eθ
−→
eϕ
−→
er
L
θ
O
Oz
(R)
ω0Oz −→ ez
(R)
−→
LOL, m, θ, ˙ θ
ω0−→
LO(S)

−−→
GM =−−−−→ M1M2
µ
d= 1,5.1011m
ms= 2.1030kg mT= 6.1024 kg
m1m2
Ep
∀α > 0,∀−→ r , Ep(α−→ r) = αkEp(−→ r)
−→
r .−−→ gradEp=kEp
< f >= lim
T→∞
1
TZT
0
f(t)dt f 2<
Ec>=k < Ep>
N
Ep(−→ r1, ..., −→ rN)
M R T
<Ec> N
C